
复变函数第一节5复变函数积分的概念一、积分的定义二、积分存在的条件及其计算法三、积分的性质四、小结与思考u
第一节 复变函数积分的概念 一、积分的定义 二、积分存在的条件及其计算法 三、积分的性质 四、小结与思考
复变函数一、积分的定义1.有向曲线:设C为平面上给定的一条光滑(或按段光滑)曲线,如果选定C的两个可能方向中的一个作为正方向(或正向),那么我们就把C理解为带有方向的曲线,称为有向曲线如果A到B作为曲线C的正向.B那么B到A就是曲线C的负向,记为C-+xu
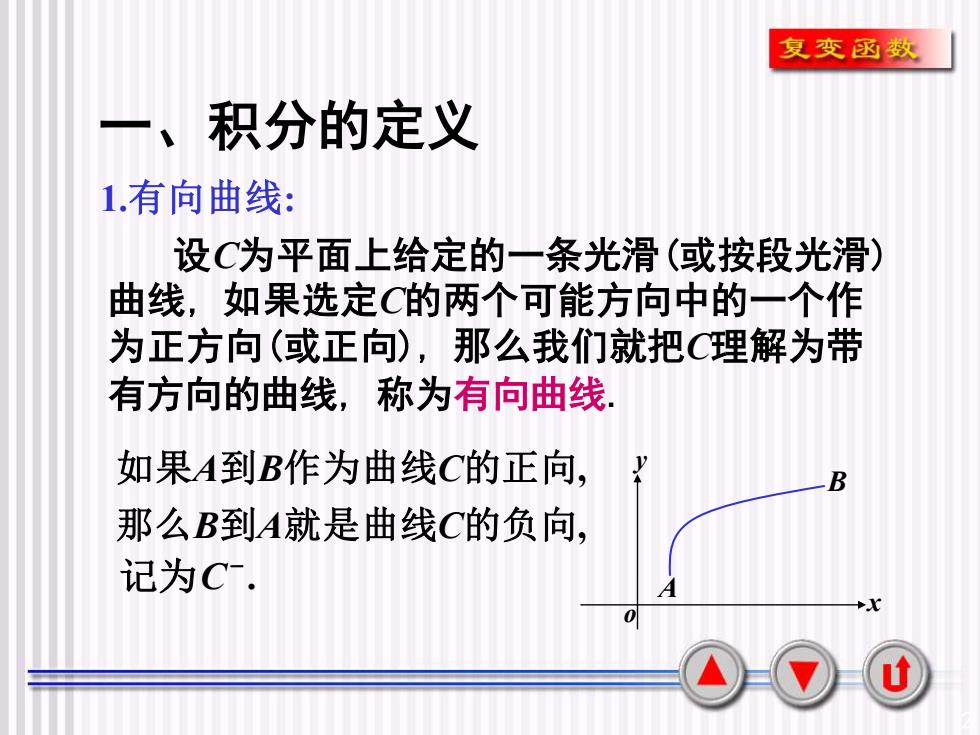
2 一、积分的定义 1.有向曲线: 设C为平面上给定的一条光滑(或按段光滑) 曲线, 如果选定C的两个可能方向中的一个作 为正方向(或正向), 那么我们就把C理解为带 有方向的曲线, 称为有向曲线. x y o A 如果A到B作为曲线C的正向 B , 那么B到A就是曲线C的负向, . − 记为C
复变函数关于曲线方向的说明:在今后的讨论中,常把两个端点中的一个作为起点,另一个作为终点,除特殊声明外,正方向总是指从起点到终点的方向简单闭曲线正向的定义:简单闭曲线C的正向是指当曲线上的点P顺此方向前进时,邻近P点的曲线x的内部始终位于P点的左方与之相反的方向就是曲线的负方向u
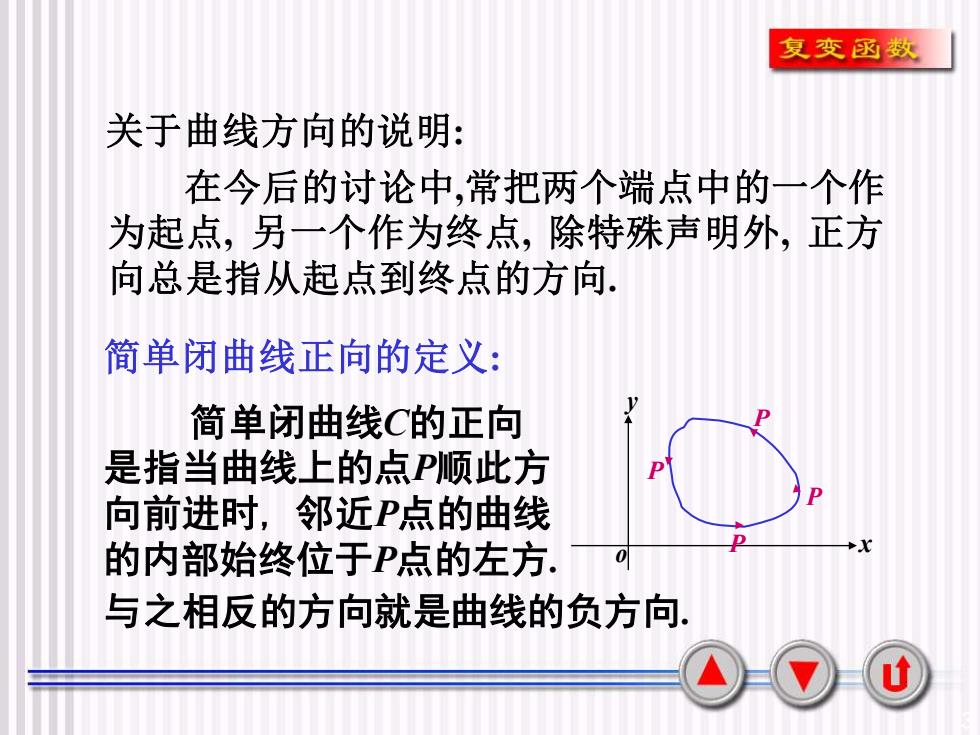
3 简单闭曲线正向的定义: 简单闭曲线C的正向 是指当曲线上的点P顺此方 向前进时, 邻近P点的曲线 的内部始终位于P点的左方. x y o P P P P 与之相反的方向就是曲线的负方向. 关于曲线方向的说明: 在今后的讨论中,常把两个端点中的一个作 为起点, 另一个作为终点, 除特殊声明外, 正方 向总是指从起点到终点的方向
复变函数2.积分的定义:设函数w = f(z)定义在区域D内,C为区域D内起点为A终点为B的一条光滑的有向曲线把曲线C任意分成n个弧段,设分点为A= Zo, Z1, -, k-1, Zk,-, Zn = B,ByC1在每个弧段zk-1zkZ.n-1CH(k = 1,2,.,n)TS.s.Zk-1上任意取一点5k22AZ0u
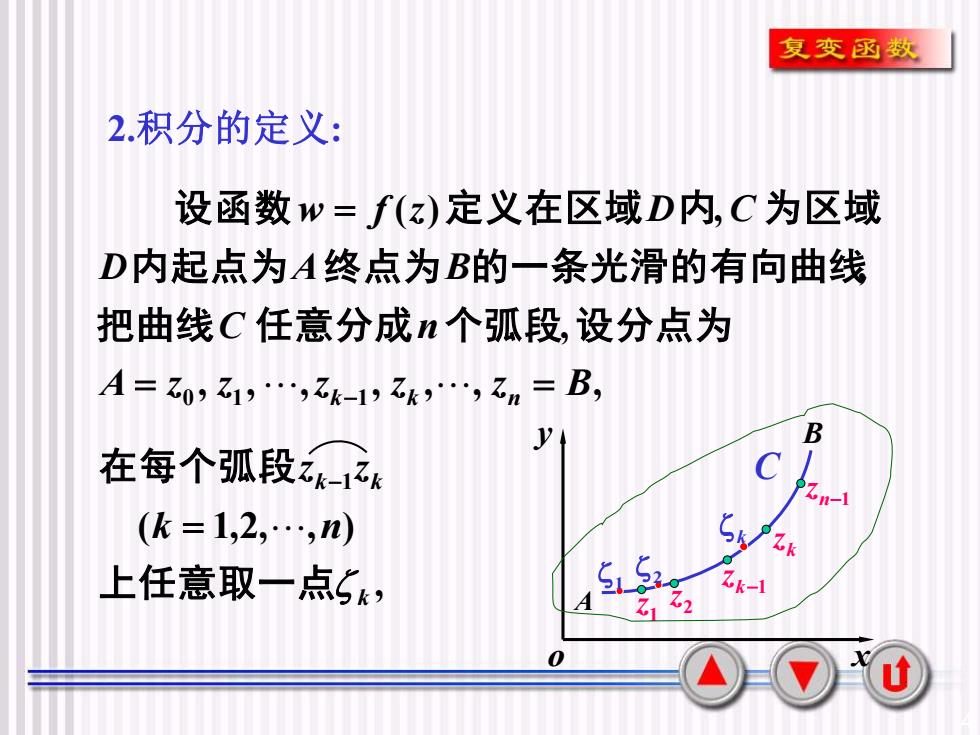
4 2.积分的定义: , , , , , , , , , ( ) , A z0 z1 z 1 z z B C n D A B w f z D C = k k n = = − 把曲线 任意分成 个弧段 设分点为 内起点为 终点为 的一条光滑的有向曲线 设函数 定义在区域 内 为区域 o x y A B n−1 z k z k−1 z 2 z 1 z k C 1 2 , ( 1,2, , ) 1 k k k k n z z 上任意取一点 在每个弧段 = −
复变函数作和式 S,=f(S)·(zk=zk-1)=f(5k)△zk)k=1k=1这里△z= zZk-1,ASk=zk的长度,记s=max[△s,当n无限增加且S→0时,1≤k≤n如果不论对C的分法及的取法如何,S.有唯一极限,那么称这极限值为B函数f(z)沿曲线C的积分;C1Zzn-1记为CHTS. S?Zf(Sk)AzkZk-1(Cf(z)dz = lim22Zn-→>0k=10U
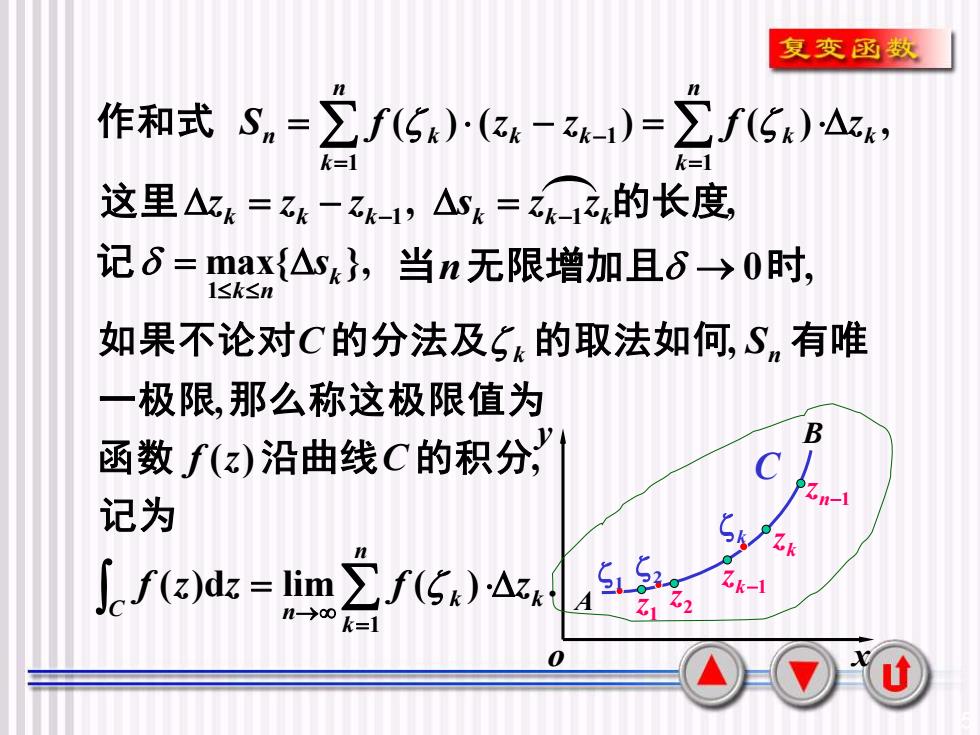
5 ( ) ( ) ( ) , 1 1 1 k n k k n k n k k k S = f z − z = f z = = 作和式 − o x y A B n−1 z k z k−1 z 2 z 1 z k C 1 2 max{ }, 1 k k n = s 记 , , 这里zk = zk − zk−1 sk = zk−1 zk的长度 当n无限增加且 → 0时, ( ) , , , 记 为 函 数 沿曲线 的积分 一极限 那么称这极限值为 如果不论对 的分法及 的取法如何 有 唯 f z C C k Sn ( )d lim ( ) . 1 k n k k C n f z z = f z = →