《复变函数与积分变换》课程教学资源（PPT课件）第二章 解析函数 2.0 习题课

复变函数第二章解析函数一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点：1.解析函数的概念；2.函数解析性的判别难点：1.解析函数的概念;2.初等函数中的多值函数及主值的概念

2 一、重点与难点 重点： 难点： 1. 解析函数的概念； 2. 函数解析性的判别 1. 解析函数的概念； 2. 初等函数中的多值函数及主值的概念

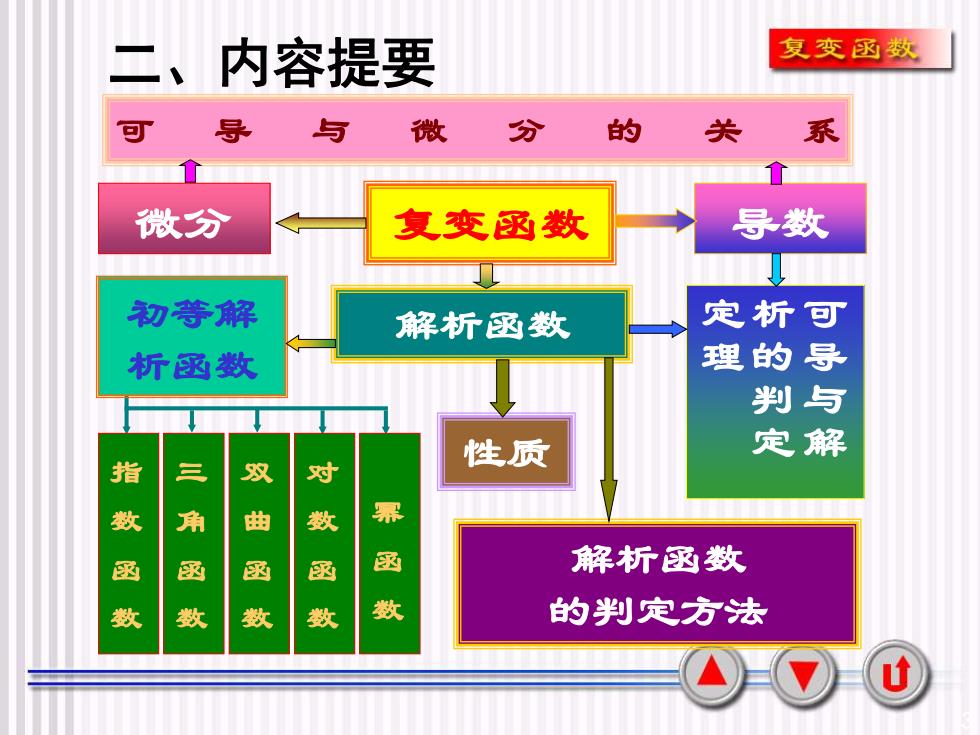
复变函数二、内容提要可导与微分的关系微分导数复变函数初等解定析可解析函数理的导析函数与判定解性质指双曲对三角函旧数函幕数函函数解析函数函数一数的判定方法数数U

3 二、内容提要 微分 复变函数 导数 初等解 解析函数 析函数 指 数 函 数 三 角 函 数 对 数 函 数 幂 函 数 性质 解析函数 的判定方法 可导与微分的关系 可 导 与 解 析 的 判 定 定 理 双 曲 函 数

复变函数1.复变函数的导数与微分1）导数的定义设函数w= f(z)定义于区域D,z为D中的一点,点zo +△z不出D的范围,如果极限f(zo + △z) - f(zo)limAzAz-0存在,那么就称f(z)在z.可导.这个极限值称为f(z)在z的导数,记作dwf(zo + △z) - f(zo)= limf'(zo) =dz.AzAz-→0Z=Z0U

4 1）导数的定义 . ( ) ( ) lim d d ( ) , , ( ) . ( ) ( ) ( ) lim , , ( ) , 0 0 0 0 0 0 0 0 0 0 0 0 z f z z f z z w f z z f z z f z z f z z f z z z D w f z D z D z z z z  +  −  = =  +  − +  =  → =  → 在 的导数 记作 存在 那么就称 在 可导 这个极限值称为 点 点 不出 的范围 如果极限 设函数 定义于区域 为 中的一 1. 复变函数的导数与微分

复变函数定义如果函数f(z)在区域D内处处可导,我们就称在区域内D可导2）可导与连续函数f(z)在z 处可导则在z 处一定连续,但函数,）在Z处连续不一定在处可导3）求导公式与法则(1）（c）=0，其中c为复常数（z"）= nz"-l，其中n为正整数(2)(3)f(z)±g(z)) = f'(z)±g'(z)u

5 . ( ) , 称在区域内 可导 如果函数 在区域 内处处可导 我们就 D 定 义 f z D 2)可导与连续 函数 f (z) 在 z0 处可导则在 z0 处一定连续, 但 函数 f(z) 在 z0 处连续不一定在 z0 处可导. 3)求导公式与法则 (1) (c) = 0, 其中c为复常数.  (2) ( ) , . z n  = nzn−1 其中n为正整数 (3) [ f (z) g(z)] = f (z)  g(z).  