
复变函数第四章级数一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点:函数展开成泰勒级数与洛朗级数难点:函数展开成洛朗级数
2 一、重点与难点 重点: 难点: 函数展开成泰勒级数与洛朗级数 函数展开成洛朗级数
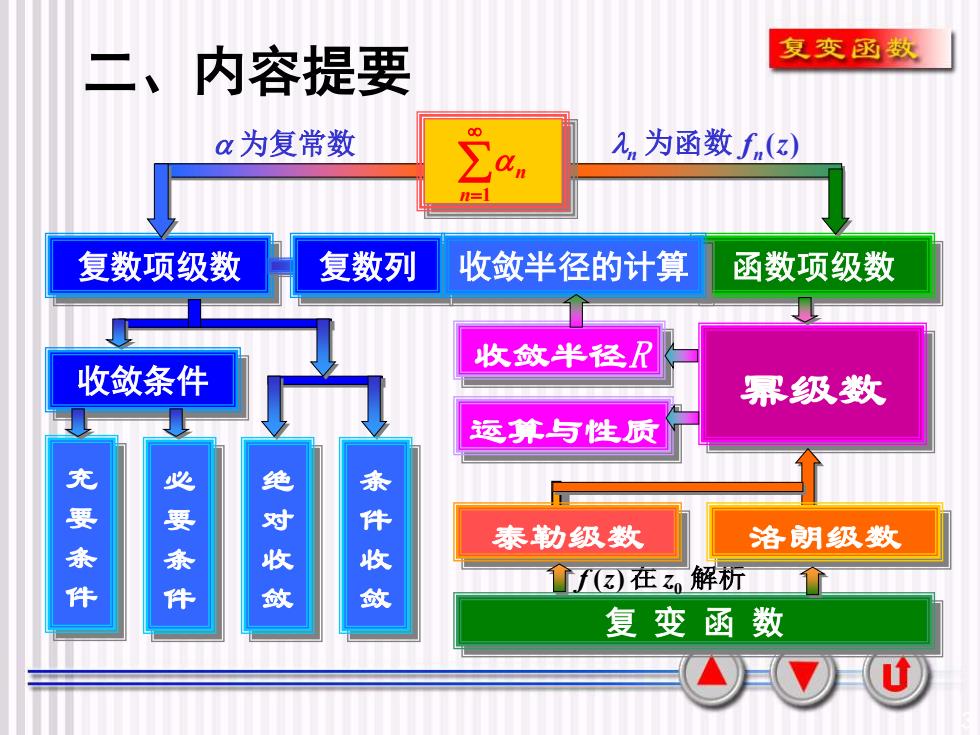
复变函数二、内容提要00α为复常数a,为函数 f,(z)Za复数列复数项级数收敛半径的计算函数项级数收敛半径R收敛条件幂级数运算与性质充要条件必要条件绝对收敛条件收敛泰勒级数洛朗级数f()在Z解析复变函数山
3 复数项级数 函数项级数 充 要 条 件 必 要 条 件 幂级数 收敛半径R 复 变 函 数 绝 对 收 敛 运算与性质 f (z) 在 z0 解析 为复常数 f (z) n 为函数 n n=1 n 收敛条件 条 件 收 敛 复数列 收敛半径的计算 泰勒级数 洛朗级数 二、内容提要

复变函数1.复数列设{α}(n=1,2,)为一复数列其中αn=an+ibn,又设α=a+ib为一确定的复数如果任意给定ε>0,相应地都能找到一个正数N(),使αn-α<ε在n>N时成立,那末α称为复数列iα,当n→8时的极限记作limαn =α.n->00此时也称复数列α,收敛于αu
4 1.复数列 如果任意给定 0,相应地都能找到一个正数 N( ),使 在n N 时成立, n − 那末 称为复数列{ }当n → 时的极限, n 记作 lim = . → n n 此时也称复数列{ }收敛于. n 设{ } (n = 1,2, )为一复数列,其中 n , n n n = a + ib 又设 = a + ib为一确定的复数

复变函数2.复数项级数1)定义设(αn} ={an+bn}(n=1,2,.)为一复数列8Z表达式αu=α,+α,+..+αn +..Rnn=1称为复数项无穷级数部分和其最前面 n项的和sn=α +αz++α,称为级数的部分和u
5 = + ++ + = n n n 1 2 1 表达式 称为复数项无穷级数. 其最前面 n 项的和 n n s = 1 + 2 ++ 称为级数的部分和. 部分和 2.复数项级数 设{ } = {a + b }(n = 1,2, )为一复数列, 1) 定义 n n n