
重积分第十章第二节二重积分的计算法,利用直角坐标计算二重积分二、利用极坐标计算二重积分0
第十章 重积分 第二节 二重积分的计算法
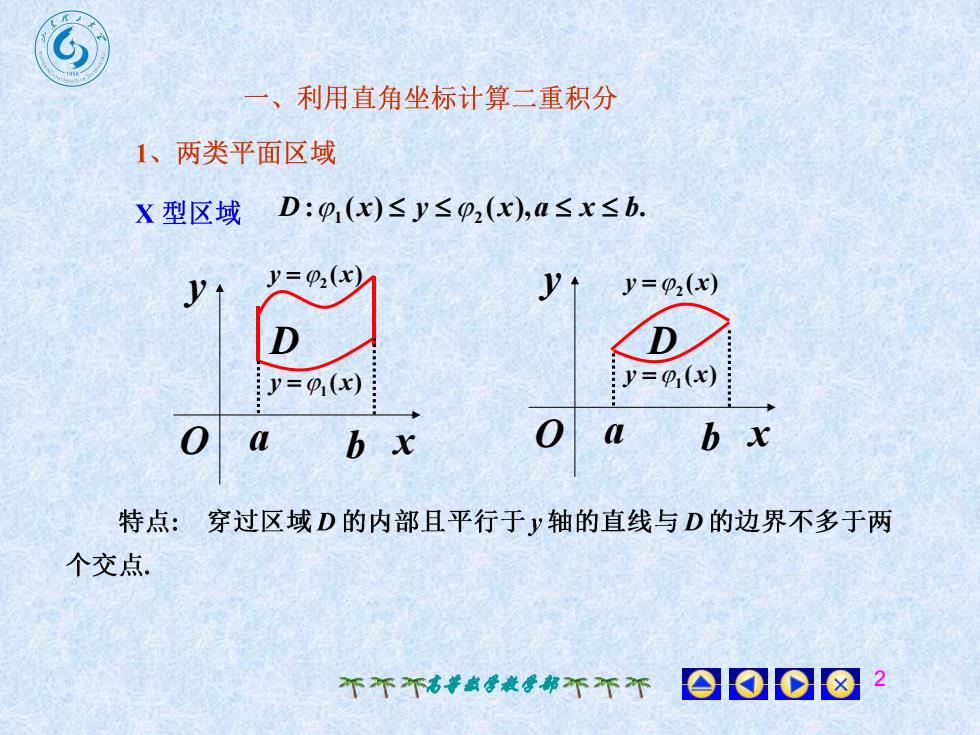
一、利用直角坐标计算二重积分1、两类平面区域D:p(x)≤y≤p,(x),a≤x≤b.X 型区域y= P2(x)Vy= P2(x)VDDy=@(x)y=p(x)0abx0ab x特点:多穿过区域D的内部且平行于y轴的直线与D的边界不多于两个交点.000个不个高数学教学部不不个
高等数学教学部 2 : ( ) ( ), . D 1 x y 2 x a x b x y O a b ( ) y 1 x ( ) y 2 x D x y O a b ( ) y 1 x ( ) y 2 x D
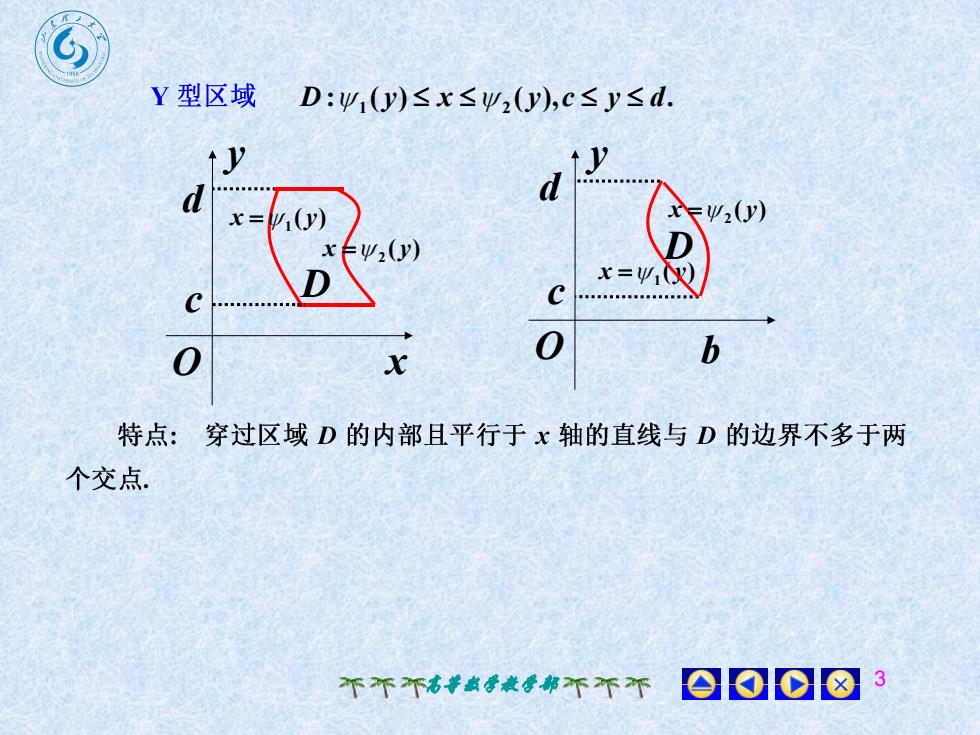
Y型区域D:y.(y)≤x≤y,(y),c≤y≤d.yJddV2(y)x=W.(y)DEy2(y)Xx=业XDCC0b0x特点:穿过区域D的内部且平行于x轴的直线与D的边界不多于两个交点.200不不不高等数学教学部不不个
高等数学教学部 3 : ( ) ( ), . D 1 y x 2 y c y d x y O c d ( ) 1 x y ( ) 2 x y D d y O c b ( ) 1 x y ( ) 2 x y D
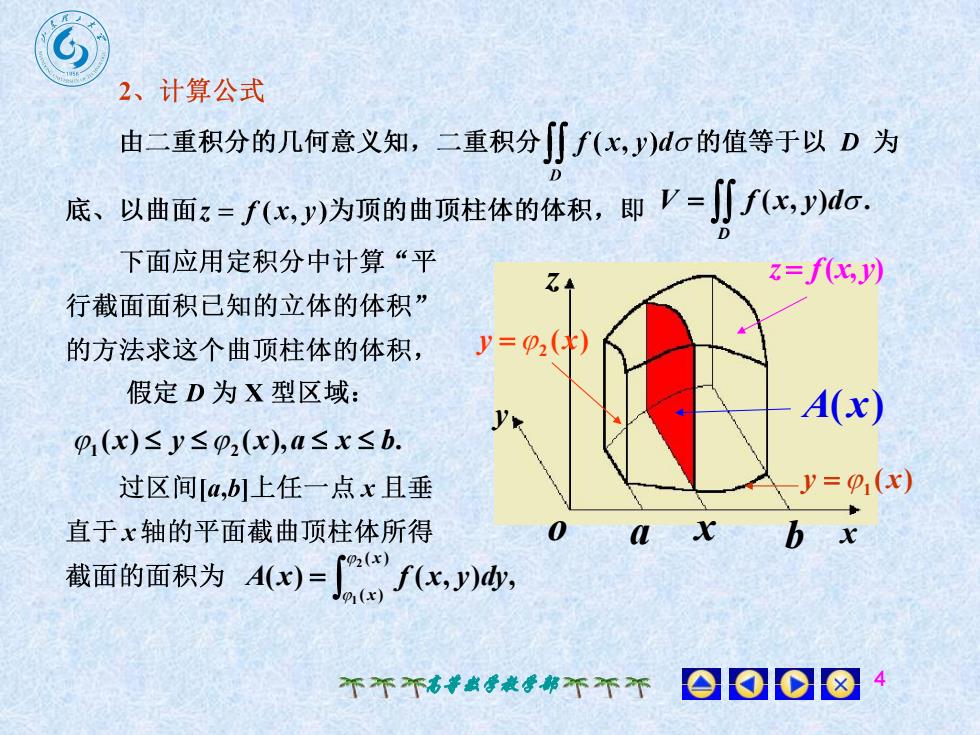
2、计算公式由二重积分的几何意义知,二重积分[f(x,y)do的值等于以 D 为底、以曲面z=f(x,y)为顶的曲顶柱体的体积,即 V=J f(x,y)do.0下面应用定积分中计算“平z=f(x,Jy)Z4行截面面积已知的立体的体积”y=02(X)的方法求这个曲顶柱体的体积,假定D为X型区域:A(x)P(x)≤y≤P2(x),a≤x≤b.y=P(X)过区间[a,b]上任一点x且垂0直于x轴的平面截曲顶柱体所得Xbxa0(x截面的面积为 A(x)=f(x, y)dy,0x0008个个个高等数学教学部不不个
高等数学教学部 4 z y o a x b x A(x) z f(x, y) ( ) 1 y x ( ) 2 y x ( , ) . D V f x y d ( ) ( ), . 1 x y 2 x a x b ( ) ( , ) , ( ) ( ) 2 1 x x A x f x y dy
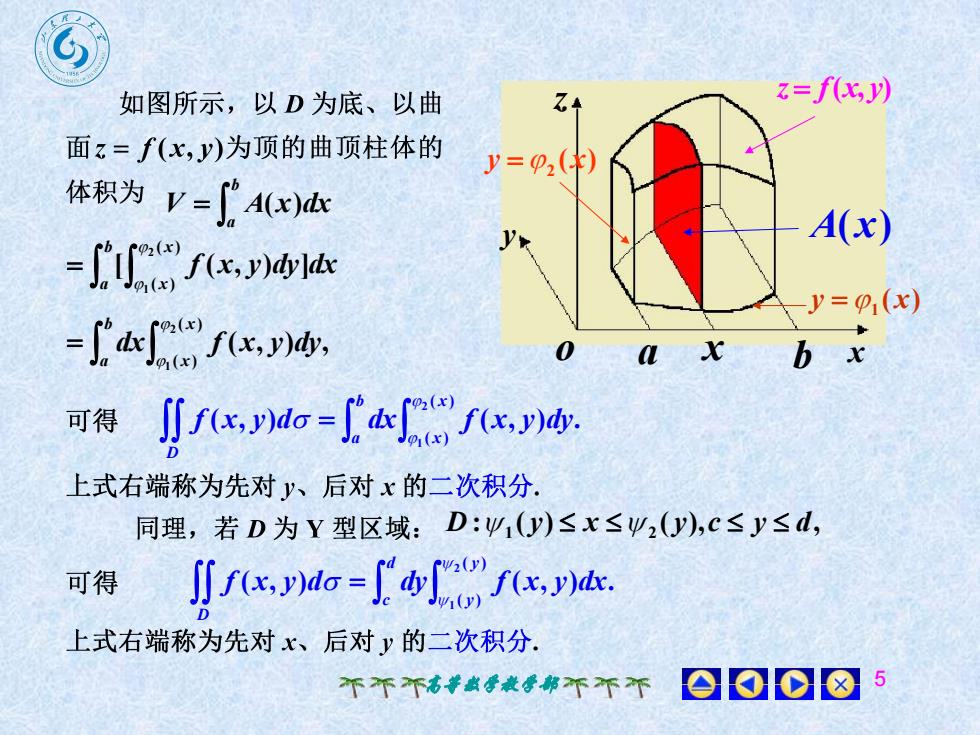
Sz=f(x,y)Z.如图所示,以D为底、以曲面z= f(x,y)为顶的曲顶柱体的y=(P2()体积为 V=' A(x)dxA(x)-'10(m f(x, )dy]axy=p(x)-I'dx n() (x,y)dy,0axbx[J f(x, y)do =I' dx [o(m) f(x, )dy.可得上式右端称为先对y、后对x的二次积分同理,若D为型区域:D:yi(y)≤x≤2(y),c≤y≤d,J f(x,y)do =I' dym) f(x, y)dx.可得上式右端称为先对x、后对的二次积分0008个不不高等数学教学部不不
高等数学教学部 5 z y o a x b x A(x) z f(x, y) ( ) 1 y x ( ) y 2 x b a V A(x)dx b a x x [ f (x, y)dy]dx ( ) ( ) 2 1 ( , ) , ( ) ( ) 2 1 b a x x dx f x y dy ( , ) ( , ) . ( ) ( ) 2 1 D b a x x f x y d dx f x y dy : ( ) ( ), , D 1 y x 2 y c y d ( , ) ( , ) . ( ) ( ) 2 1 D d c y y f x y d dy f x y dx