《高等数学》课程教学资源（课件讲稿）第十一章 曲线积分与曲面积分_1106高斯公式

第十一章曲线积分与曲面积分第六节高斯公式高斯公式08

第十一章 曲线积分与曲面积分 第六节 高斯公式

-高斯公式定理1设空间闭区域Q由分片光滑的闭曲面围成，函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Q上具有一阶连续偏导数， 则有公式apaQaRJS)dv = [[ Pdydz + Qdzdx + RdxdyaxayozQNapaRaQ5)dv= ff(Pcosα + Qcos β + Rcos )ds,axayazO7这里Z是Q的整个边界曲面的外侧，cosα,cosβ,cosy是乙上点(x,y,z)处的法向量的方向余弦说明高斯公式表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系00l08不不不高尊数学教学部不不不

高等数学教学部 2 ( )dv (P cos Qcos Rcos )dS, z R y Q x P                  

分析欲证apaQaRJ)dv-f Pdydz + Qdzdx + RdxdyOzayaxQXR-α川a=ff R(x, y,z)dxdydy只需证JEpaaZv=}f P(x, ,z)dydAaQdv=fo(x, y,z)dzdxay2Moog个个个高等数学教学部个不个

高等数学教学部 3                dv Pdydz Qdzdx Rdxdy z R y Q x P ( )        dv R x y z dxdy z R ( , , )        dv P x y z dydz x P ( , , )        dv Q x y z dzdx y Q ( , , )

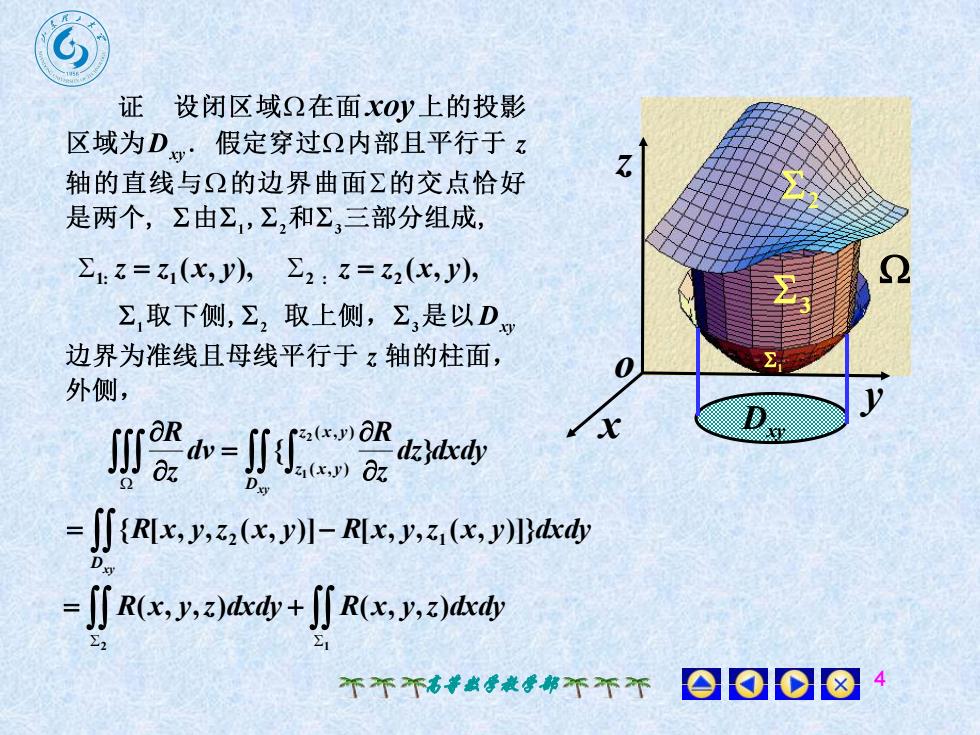
证设闭区域Q在面xoy上的投影区域为D：假定穿过Q内部且平行于z7.公心轴的直线与Q的边界曲面的交点恰好是两个，Z由Z，Z,和Z，三部分组成2E1.z = zi(x, y), E2 : z =z2(x,y),Z,取下侧,Z，取上侧，Z,是以D边界为准线且母线平行于z轴的柱面，0外侧,yxaRw-dzjdxdyaz2Dxy- J] (R[x, y,z,(x, y)]- R[x, y,z(x, y)]]dxdy1Dxy- [[ R(x, y,z)dxdy + [[ R(x, y,z)dxdy222001018个不不高教学教学部不不不

高等数学教学部 4 x y z o ( , ), 1: 1  z  z x y ( , ), 2 : 2  z  z x y  1 2 3 Dxy dz dxdy z R dv z R Dxy z x y   z x y       { } ( , ) ( , ) 2 1    Dxy {R[x, y,z (x, y)] R[x, y,z (x, y)]}dxdy 2 1     2 1 ( , , ) ( , , )   R x y z dxdy R x y z dxdy

?[[ R(x, y,z)dxdy + [[ R(x, y,z)dxdy + [[ R(x, y,z)dxdy223JITORdv =ff R(x, y,z)dxdy,= jf R(x, y,z)dxdy,azZQA如果穿过Q内部且平行于x轴以及平行于轴的直线与Q的边界曲面Z的交点也恰好是两个，类似地有10o- prIra -f la,./ita.ZOapaQ + OR)adv- f Plyd + Qdadx + Rdxdy.JaxayOzQ由两类曲面积分之间的关系知apaQaR台J)dv= ff(Pcosα + Qcos β+ Rcos y)ds.axazay2o08个不不高教学教学部不不不

高等数学教学部 5     2 1 ( , , ) ( , , )   R x y z dxdy R x y z dxdy   3 ( , , )  R x y z dxdy ( , , ) ,    R x y z dxdy ( , , ) ,         dv R x y z dxdy z R ( , , ) ,        dv P x y z dydz x P ( , , ) ,        dv Q x y z dzdx y Q ( ) .                 dv Pdydz Qdzdx Rdxdy z R y Q x P ( ) ( cos cos cos ) .                dv P Q R dS z R y Q x P   