
第七章曲线积分与曲面积分第三节格林公式及其应用格林公式福二、平面上曲线积分与路径无关的条件三、二元函数的全微分求积08
第七章 曲线积分与曲面积分 第三节 格林公式及其应用
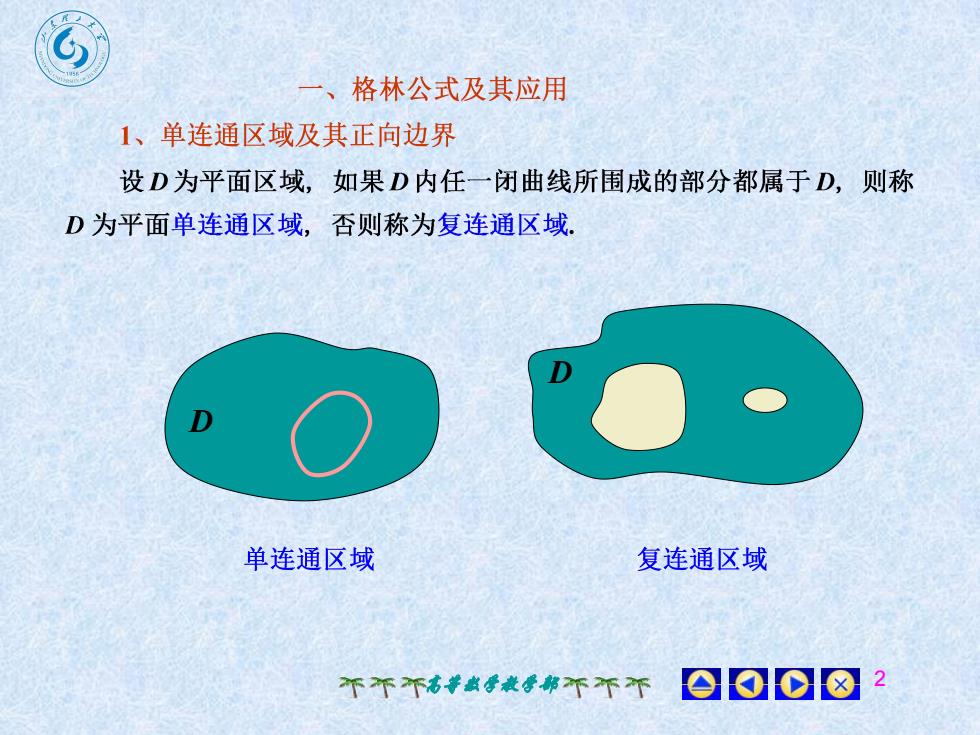
格林公式及其应用1、单连通区域及其正向边界设D为平面区域,如果D内任一闭曲线所围成的部分都属于D,则称D为平面单连通区域,否则称为复连通区域D单连通区域复连通区域001018个不不高等数学教学部不不不
高等数学教学部 2 D D
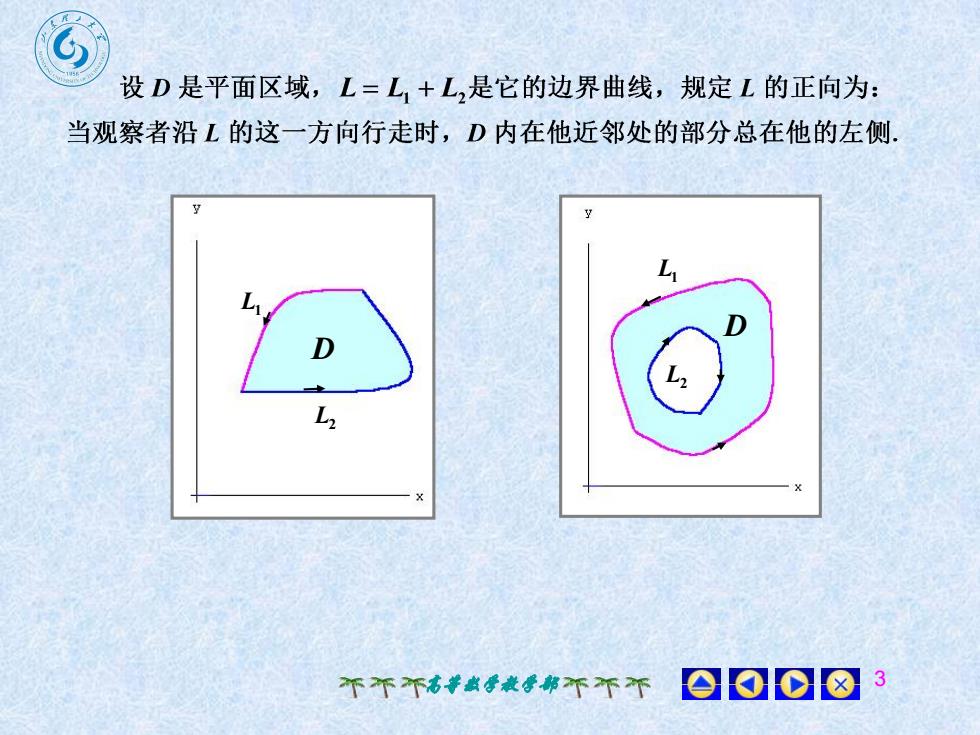
设D是平面区域,L=L,+L,是它的边界曲线,规定L的正向为当观察者沿L的这一方向行走时,D内在他近邻处的部分总在他的左侧D0018不不不高数学教学部不不不
高等数学教学部 3 L2 D L1 L2 L1 D

2、格林公式定理 1设闭区域D由分段光滑的曲线L围成,函数P(x,J)及Q(x,y)aQ ap在 D上具有一阶连续偏导数, 则有[,Pdx+Qdy= J()dxdy(1)ayaxn其中L是D的取正向的边界曲线公式(1)叫做格林公式,它表明了沿闭区域边界L的曲线积分可以通过平面闭区域D上的二重积分来表达apaQf, Pdx+ Qdy= J](分析 欲证)dxdyaxayDTrap只需证fPdx=-dxdyJDaya0福f.oly-JldxdyaxD001018个个高等数学教学部个不个
高等数学教学部 4 D L dxdy yP xQ Pdx Qdy ( ) D L dxdy yP Pdx D L dxdy xQ Qdy

证先假设穿过区域D内部且平行于坐标轴的直线与D的边界不多于两个交点,即区域D既是X型又是Y型因D是X型区域,故可表示为D =((x,y)pi(x)≤y≤p,(x),a≤x≤b)L, : y = P,(x)Jo-agDB=I' P(x,P,(x)dx-I" P(x,pi(x)dxL : y= p(x)=-f P(x, P,(x)dx-' P(x,p(x)dxXb=-J, P(x,J)dx-J, P(x,y)dxJ% d-f x d(2)--f P(x,y)dx,ayD00108个不高等数学教学部不不不
高等数学教学部 5 y x o a b D : ( ) L1 y 1 x : ( ) L2 y 2 x A B dy y P dxdy dx y P x x b a D ( ) ( ) 2 1 b a b a P(x,2 (x))dx P(x,1 (x))dx 2 1 ( , ) ( , ) L L P x y dx P x y dx ( , ) , L P x y dx ( , ) . (2) L D dxdy P x y dx y P b a a b P(x,2 (x))dx P(x,1 (x))dx {( , ) ( ) ( ), }. D x y 1 x y 2 x a x b