《高等数学》课程教学资源（课件讲稿）第十二章 级数_1202常数项级数的审敛法

第十二章无穷级数第二节宫常数项级数的审敛法正项级数及其审敛性交错级数及其审敛性国三华绝对收敛与条件收敛08

第十二章 无穷级数 第二节 常数项级数的审敛法 一、正项级数及其审敛性 二、交错级数及其审敛性 三、绝对收敛与条件收敛

?一、正项级数及其审敛性每一项都是常数的级数称为常数项级数，每一项都大于或等于零的常数项级数称为正项级数若u.=u, +u, + u, +.+u, +...为正项级数,则部分和数列说明{S,}: S, = u, +u, +u, +...+u,单增.1、基本定理定理 1（基本定理）正项级数u，=u +u,+u,+.+u,+..收敛的充分必要条件是它的部分和数列(S，有界设正项级数u,=u, +u, +u,+….+u,+.收敛,证（必要性）n=即部分和数列(S,}收敛，因而{S,}有界Zu,也收敛.（充分性）设{S,有界,又{S,}单增，故{S,收敛,=0010182不不高等教学教学部不不

高等数学教学部 2

+2、比较审敛法设u,和v，是两个正项级数，且定理 2 （比较审敛法）n=1n=1u, ≤ v,(n = 1,2,...).(1）若v,收敛，则u,收敛；（2）若u,发散，则v,发散n=ln=1n=8证 记u,部分和为S,，,部分和为o,又u,≤vn,S,≤o,n=ln=18080Z.u,收敛Zv,收敛，知[o,)有界，故[S,)有界，级数因(1)三u,发散，知(S,)无界，故(o,)无界，级数因V,发散.(2)n=1n=14008个个个高数学教学部不不个

高等数学教学部 3

设u,和v,是两个正项级数，且存在正整数 N，当n>N推论n=1n=1时有u,≤kv,，k为正常数(1）若v,收敛，则u,收敛；(2）若u,发散，则v,发散n=1:说明使用比较判别法判断级数的收敛性，须掌握一些重要级数的收敛性，如几何级数、调和级数、p级数等．这是一种利用已知级数判别未知级数的方法001018个不个高尊数学教学部不不不

高等数学教学部 4

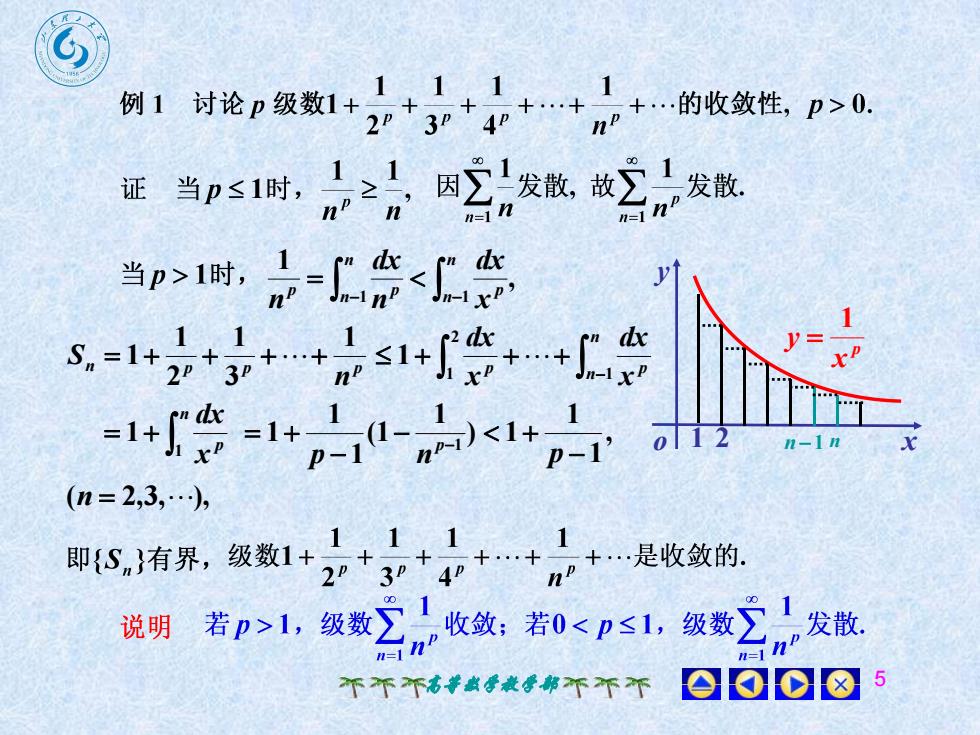
例 1 讨论 p 级数1 +..的收敛性，p>03P2p480001ZZ因发散，故发散证当p≤1时,hn=innnn=1dx-广广会当p>1时,V.dxd+. ...+x一12F-1xdxp--)<1+=1+1-0112xn-in1(n = 2,3,...),1是收敛的即{S,}有界，级数1+2D3402发散.若p>1，级数收敛；若0<p≤l，级数说明n=eoo8个个个高等数学教学部个不个

高等数学教学部 5 , 1  1  1   n n p n n p p x dx n dx n n p p p n S 1 3 1 2 1  1          n n p p x dx x dx 1 2 1 1     n p x dx 1 1 ) 1 (1 1 1 1 1     p p n , 1 1 1    p o y x p x y 1  1 2 n  1 n (n  2,3,)