
说明(1)将二重积分化为二次积分时,确定积分限是一个关键,1应先画出积分区域D的图形.若D为X型区域,可先在x轴上取一点并过该点作轴的平行线,则该直线与D的边界的两个交点的纵坐标便为y的积分限,而D内点的最小横坐标、最大横坐标便为x的积分限,二重积分可以化为先对y、后对x的二次积分同样地,若D为Y型区域,可先在轴上任取一点y并过该点作x轴的平行线,则该直线与D的边界的两个交点的横坐标便为x的积分限,而D内点的最小纵坐标、最大纵坐标便为的积分限,二重积分可以化为先对x、后对的二次积分(2)如果积分区域 D 既不是X 型的,也不是 Y 型的.可用 x轴或轴的平行线将D分割成若干小区域,使每个小区域属于X型的或Y型的,使用(1)的方法计算出每个小区域上的二重积分,再相加即可0010个不不高数学教学部不不不
高等数学教学部 6

新(3)交换积分次序的一般方法:I'axn() (x,)dy-JJ (x,y)do -"'d) (x, )dx,其中D:P,(x)≤y≤P,(x),a≤x≤b.'mo) (x,y)dx -IJ (x, )do -I'dx() f(x, )d,其中D:,(y)≤x≤,(y),c≤y≤d.yy=P2(x)yay.(y)x=Dxt(V,(y)y=p(x)Dc0ab x0x001018个不不高等数学教学部不不
高等数学教学部 7 ( , ) , ( ) ( ) 2 1 b a x x dx f x y dy D f (x, y)d d c y y dy f x y dx ( ) ( ) 2 1 ( , ) D f (x, y)d b a x x dx f x y dy ( ) ( ) 2 1 ( , ) ( , ) , ( ) ( ) 2 1 d c y y dy f x y dx x y O c d ( ) 1 x y ( ) 2 x y D x y O a b ( ) y 1 x ( ) y 2 x D
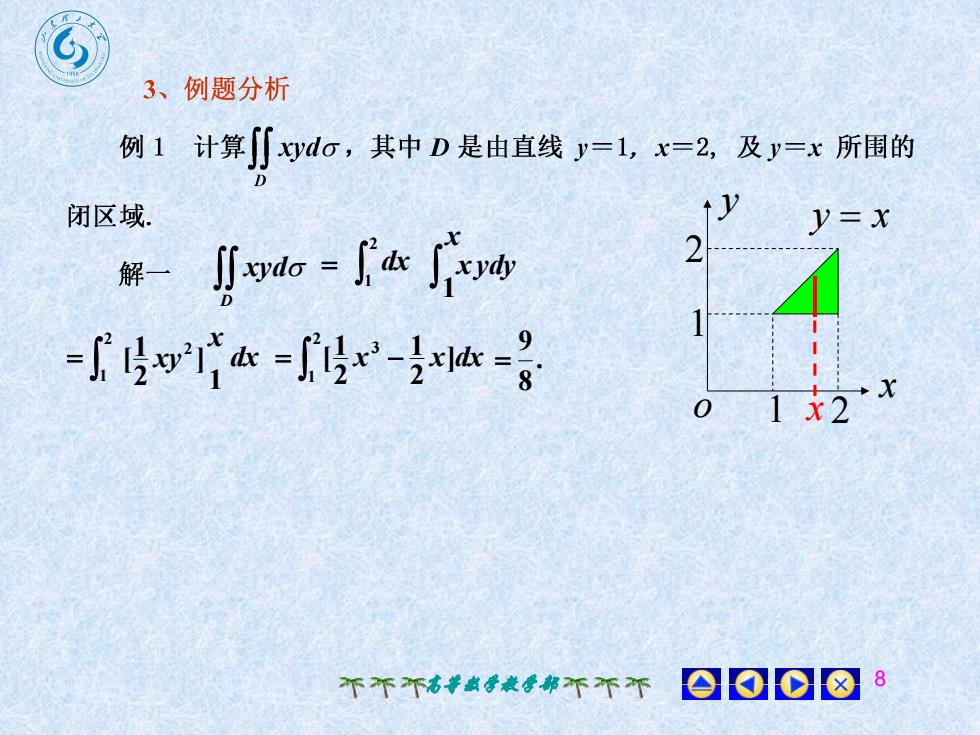
3、例题分析例 1 计算[[xydo,其中 D 是由直线 y=1,x=2,及y=x 所围的D闭区域y=x2J xdo -I'ae ixyly解一-Th,a-r-a-X0x21808个不个高等数学教学部不不不
高等数学教学部 8 x y 2 1 1 y x o 2 x D xyd 2 1 dx x ydy 2 1 dx 2 1 3 ] 2 1 2 1 [ x x dx . 8 9 1 ] 2 1 [ 2 x xy 1 x
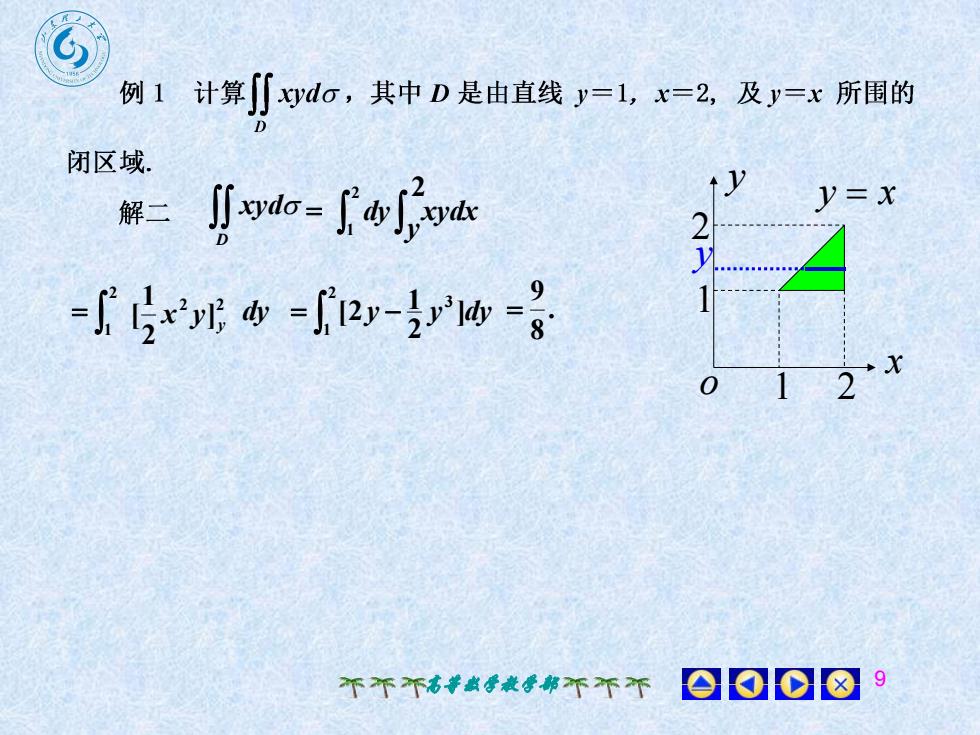
例 1 计算[[ xyd,其中 D 是由直线 y=1,,x=2,及y=x 所围的D闭区域t1y=xJxydo-f'ofiryde解二21-"5x'yl, y -'12y-2yly -X012000个不个高等数学教学部不不个
高等数学教学部 9 D xyd x y 2 1 1 y x o 2 y 2 1 dy xydx 2 1 dy 2 2] 2 1 [ y x y 2 1 3 ] 2 1 [2 y y dy . 8 9 y 2
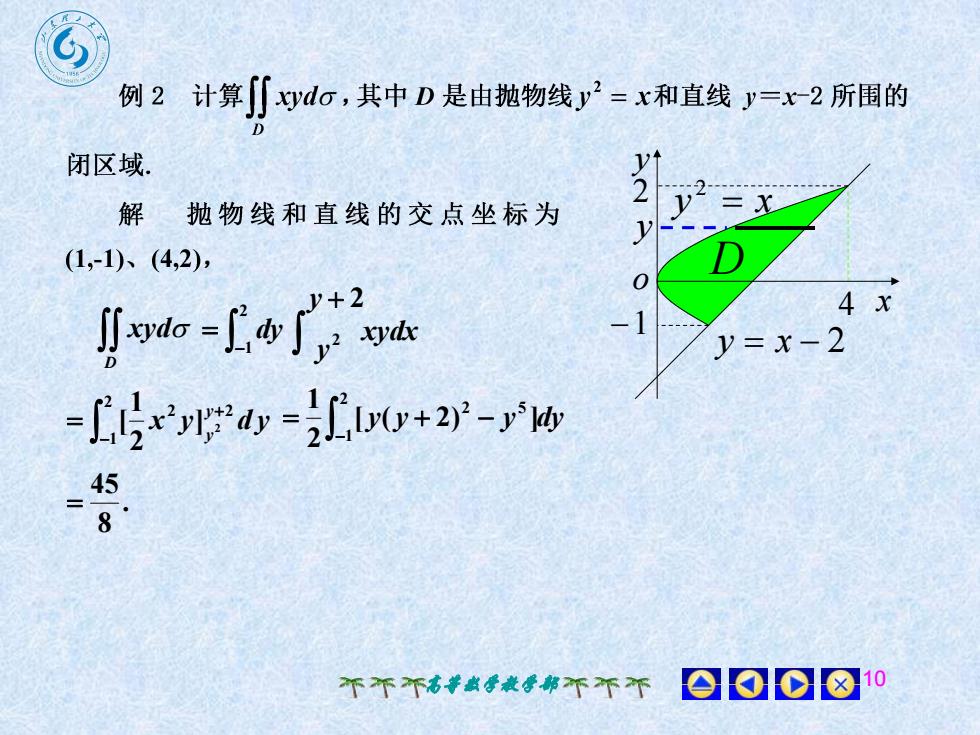
例 2 计算[[xydo,其中 D 是由抛物线y2=x和直线 y=x-2 所围的D12闭区域.V解抛物线和直线的交点坐标为y(1,-1)、(4,2),福0+24 xJ rydo - ayd-1y=x- 2L'5+ypdy -+lv(y+2)-y'my45800810不不不高数学教学部不不不
高等数学教学部 10 D y x 2 y x 2 2 1 4 o y x y D xyd xydx 2 1 dy 2 y y 2 2 1 2 2 ] 2 2 1 [ x y d y y y 2 1 2 5 [ ( 2) ] 2 1 y y y dy . 8 45