
第十一章曲线积分与曲面积分第五节对坐标的曲面积分对坐标的曲面积分的概念与性质对坐标的曲面积分的计算法三、两类曲面积分之间的联系0
第十一章 曲线积分与曲面积分 第五节 对坐标的曲面积分

?、对坐标的曲面积分的概念与性质1、有向曲面、投影假定曲面是光滑的假定考虑的曲面都是双侧的,如方程z= zx,y)表示的曲面,有上侧、下侧之分:一张封闭曲面有内侧、外侧之分,对于曲面z=z(x,),如果取它的法向量朝上,就认为取定曲面的上侧;一张封闭曲面,如果取它的法向量朝外,认为取定曲面的外侧.取定了法向量亦即取定了侧的曲面,称为有向曲面对于有向曲面Z,在Z上取一小块曲面△S,投影到xOv面上,投影区域的面积记为(△α)y假定△S上各点处的法向量与z轴的夹角的余弦同号,规定△S在xOy面上的投影(△S)为[(Ao)xycosy>0cosy<0.(AS)xy=3-(△) xy0cosy= 000108个个个高等数学教学部不个
高等数学教学部 2 . 0 cos 0 ( ) cos 0 ( ) cos 0 ( ) xy xy S xy
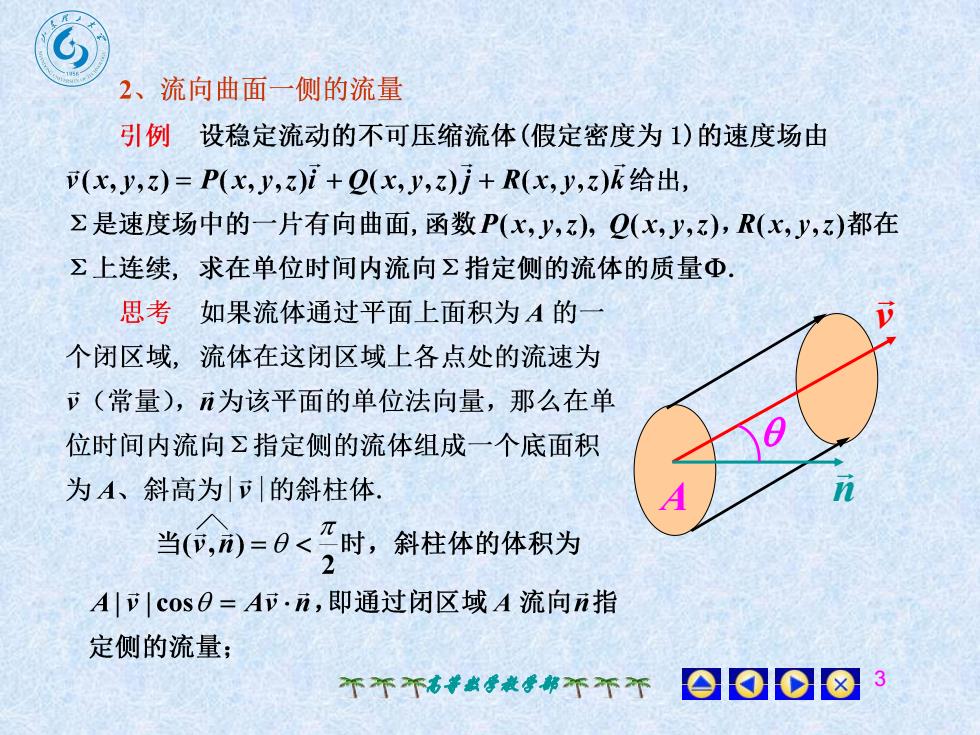
S2、流向曲面一侧的流量引例设稳定流动的不可压缩流体(假定密度为1)的速度场由(x,y,z) = P(x, y,z)i +Q(x, y,z)j+ R(x, y,z)k给出是速度场中的一片有向曲面,函数 P(x,y,z),Q(x,y,z),R(x,y,z)都在Z上连续,求在单位时间内流向指定侧的流体的质量Φ思考如果流体通过平面上面积为 A 的一V个闭区域,流体在这闭区域上各点处的流速为(常量),π为该平面的单位法向量,那么在单0位时间内流向乙指定侧的流体组成一个底面积n为A、斜高为 的斜柱体A当(,n)=<"时,斜柱体的体积为2Allcosの=Ai·n,即通过闭区域A流向n指定侧的流量;008个不高教学教学部不不不
高等数学教学部 3 v n A
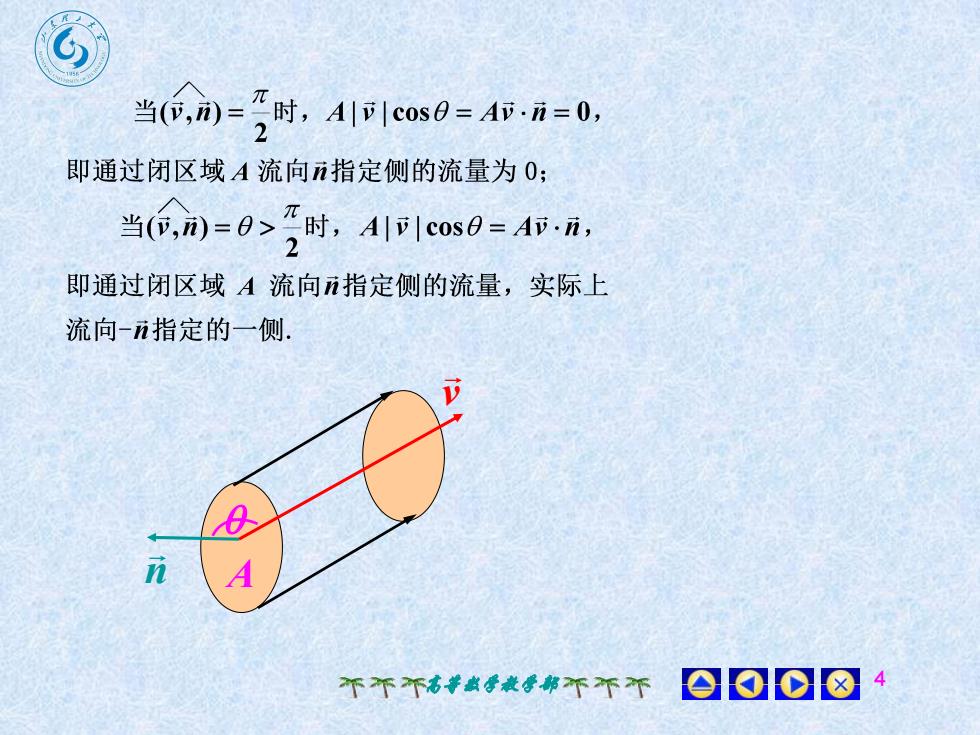
T当(,n)=一日时, A||coso=Av.n=0,2即通过闭区域A流向n指定侧的流量为0;当(D,n)=>时, A|cos=A·n,O即通过闭区域A流向n指定侧的流量,实际上流向-n指定的一侧VnA00个个个高等数学教学部
高等数学教学部 4 v n A
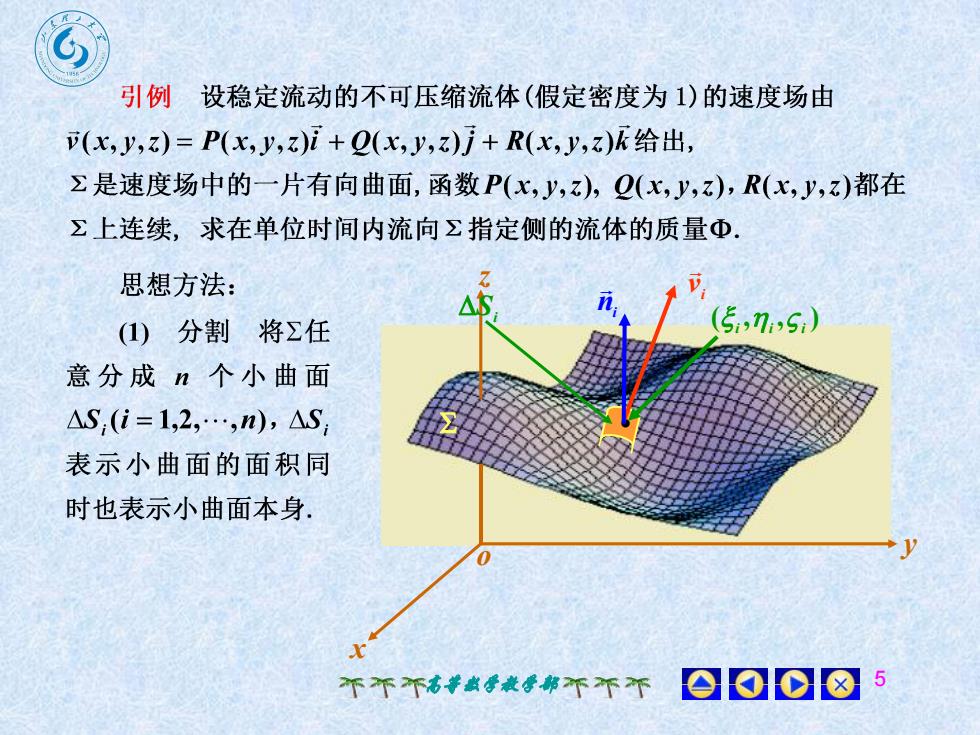
引例设稳定流动的不可压缩流体(假定密度为1)的速度场由(x, y,z)= P(x,y,z)i +Q(x, y,z)j + R(x,y,z)k给出Z是速度场中的一片有向曲面,函数P(x,y,z),Q(x,y,z),R(x,y,z)都在飞上连续,求在单位时间内流向指定侧的流体的质量Φ思想方法:(5r,ni,S.)(1)分割将Z任意分成n个小曲面AS,(i = 1,2,...,n), ASZ表示小曲面的面积同时也表示小曲面本身001018不不不高教学教学部不不
高等数学教学部 5 x y z o Si ( , , ) i i i i v ni