
第九章多元函数微分学及其应用9.4多元函数的极值人民邮电出版社RISS&HOTRES
9.4 多元函数的极值 第九章 多元函数微分学及其应用

本节内容01多元函数的极值02多元函数的最值03条件极值
本节内容 01 多元函数的极值 02 多元函数的最值 03 条件极值
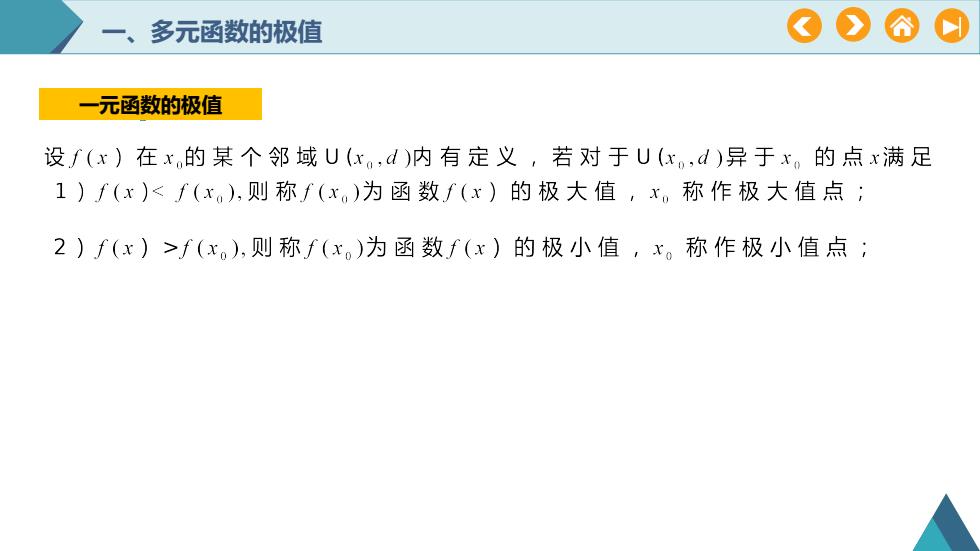
>一、多元函数的极值一元函数的极值设f(x)在x.的某个邻域U(xd)内有定义,若对于U(xd)异于x。的点x满足1)f(x)<f(x.),则称f(x。)为函数(x)的极大值x,称作极大值点;2)f(x)>f(x.)则称f(x)为函数f(x)的极小值,x。称作极小值点
一元函数的极值 一、多元函数的极值

O#0一、多元函数的极值引例Y21在点(0.0)的某邻域内函数值的变化(1)观察函数zC4(2)观察函数z=4-x2-y2在点(0.0)的某邻域内函数值的变化分析1)中,在点(0.0)的某邻域内异于(0.0)的点(x.y),有z(x, y) > z(0, 0) = 0,(2)中,在点(0,0)的某邻域内异于(0,0)的点(x),有z(x, y) <z(0, 0) = 4
引例 分析 一、多元函数的极值 z x O y z x y + = 4 9 2 2 = −x −y 2 2 z 4 z 4 x O y

M一、多元函数的极值定义9.7设函数z=f(x,y)的定义域为DiR2,P(xoy)为D的内点.若存在P(xo,yo)的某个邻域U(P)iD,对于该邻域内异于P(xo,y。)的任意点(x,y),都有f (x, y)< f (xo, yo)(或f (x, y)> f (xo, J))则称函数f(x,y)在点P(xo,J。)有极大值(或极小值)f(x,y),点P(xo,)称为函数f(x,J))的极大值点(或极小值点)极大值与极小值统称为函数的极值,使函数取得极值的点称为函数的极值点:以上关于二元函数的极值的概念,可推广到n元函数
定义9.7 一、多元函数的极值