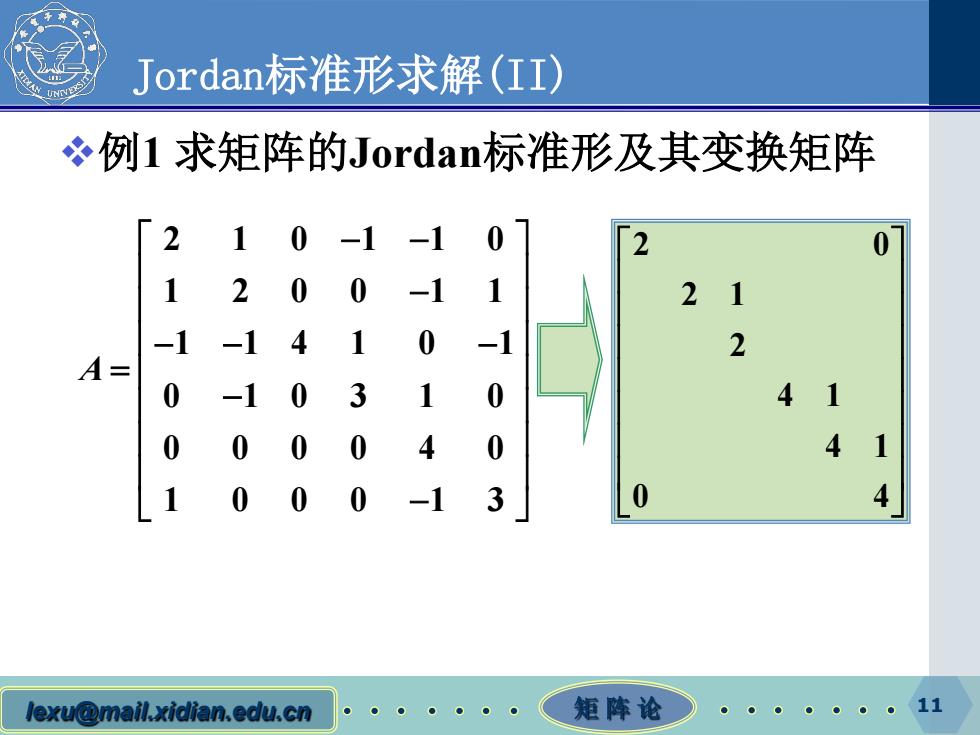
Jordan标准形求解(II) 冬例1求矩阵的Jordan标准形及其变换矩阵 2 10-1 -1 1 2 0 0 -1 21 -1 -1 4 1 0 -1 2 A= 0 -1 0 3 1 0 41 0 0 0 4 0 4 1 0 0 0 -1 3 4 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 11 Jordan标准形求解(II) 例1 求矩阵的Jordan标准形及其变换矩阵 2 10 1 10 1 200 11 1 14 1 0 1 0 10 3 1 0 0 000 4 0 1 000 13 A − − − − − − = − − 2 0 2 1 2 4 1 4 1 0 4

Jordan标准形求解(II) [解]方法二求解Jordan:标准形 ·对特征值多项式进行初等变换可得 0 (2-2) (2-2)2(2-4)3 ·可得相应初等因子组(-2),(1-2)2,(2-4) lexu@mail.xidian.edu.cn 矩阵论 12
lexu@mail.xidian.edu.cn 矩 阵 论 12 Jordan标准形求解(II) [解]方法二求解Jordan标准形 对特征值多项式进行初等变换可得 可得相应初等因子组 2 3 1 0 1 1 1 ( 2) 0 ( 2) ( 4) λ λ λ − − −

Jordan标准形求解(II) ▣得出Jordon标准形 0 2 2 41 41 10 ·且有det(2I-A)=(2-2)3(2-4)3 ·即入=2与入=4为三重特征值 lexu@mail.xidian.edu.cn 矩阵论 。。0。。。13
lexu@mail.xidian.edu.cn 矩 阵 论 13 Jordan标准形求解(II) 得出Jordon标准形 且有 • 即 为三重特征值 2 0 2 1 2 4 1 4 1 0 4 3 3 det( ) ( 2) ( 4) λ λλ I A −=− − λ λ = = 2 4 与

Jordan标准形求解(II) 冬[例2]求矩阵A的Jordan标准形 31-1 A= -2 0 2 -1-1 3 ·[解]初等变换法 ·利用初等变换将特征矩阵化为对角矩阵 ·对角线上非零多项式为f) ·由次数大于零的f)的全体不可约因式得到初等因 子组 lexu@mail.xidian.edu.cn 矩阵论 14
lexu@mail.xidian.edu.cn 矩 阵 论 14 Jordan标准形求解(II) [例2]求矩阵A的Jordan标准形 [解]初等变换法 • 利用初等变换将特征矩阵化为对角矩阵 • 对角线上非零多项式为 fi (λ) • 由次数大于零的fi (λ)的全体不可约因式得到初等因 子组 − − − − = 1 1 3 2 0 2 3 1 1 A