
场论与复变函数 主讲:徐乐
场论与复变函数 主讲:徐乐

Review 孤立奇点 若f(a)在z解析,z,为函数f的m级墨点的充要条件: 。fm(a)=0,(=0,1,2,,m-l) ·fm(z)0 奇点类型 洛朗级数 lim f(z) 零点<=>极点 2-→20 可去奇点 A)-c.- 存在且 n=0 有限:co f(z=(2-2o)"mg(2) M级极点 A()-c-a 00 若z为函数1/f(e)的m级零点, 则zo为函数f(z)的m级极点 本性奇点 f)-c- 不存在且 不为0 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 矩阵论 2 Review 孤立奇点 若f (z)在z0解析,z0为函数f (z)的m级零点的充要条件: f (n)(z0) = 0,(n=0,1,2,…,m-1) f (m)(z0) ≠0 奇点类型 洛朗级数 零点<=>极点 可去奇点 M级极点 本性奇点 0 lim ( ) z z f z 0 0 () ( )n n n f z cz z 0 -m () ( )n n n fz c z z 0 - () ( )n n n fz c z z 存在且 有限:c0 ∞ 不存在且 不为∞ f (z)=(z-z0)-mg(z) 若z0为函数1/f (z)的m级零点, 则z0为函数f (z)的m级极点

Review ·若函数fz)在无穷远点x=oo的去心领域R<z<+oo内 解析,则称点o为fz)的孤立奇点 ■作变换t=1z ·将去心领域R<zk+oo内对函数fz的研究化为在去心领域 0<k1/R内对函数p()的研究 ·显然()在去心领域0<<1/R解析,仁0为函数(⑩的孤立奇点 ·若t=0是p()的可去奇点、m级极点或本性奇点,则称 点z=oo是fz)的可去奇点、m级极点或本性奇点 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 3 Review 若函数f(z)在无穷远点 z=∞的去心领域R<|z|<+ ∞内 解析,则称点∞为f(z)的孤立奇点 作变换 t = 1/z • 将去心领域R<|z|<+ ∞内对函数f(z)的研究化为在去心领域 0<|t|<1/R内对函数φ(t)的研究 • 显然φ(t)在去心领域0<|t|<1/R解析,t=0为函数φ(t)的孤立奇点 若 t =0是φ(t)的可去奇点、m级极点或本性奇点,则称 点z=∞是f(z)的可去奇点、m级极点或本性奇点
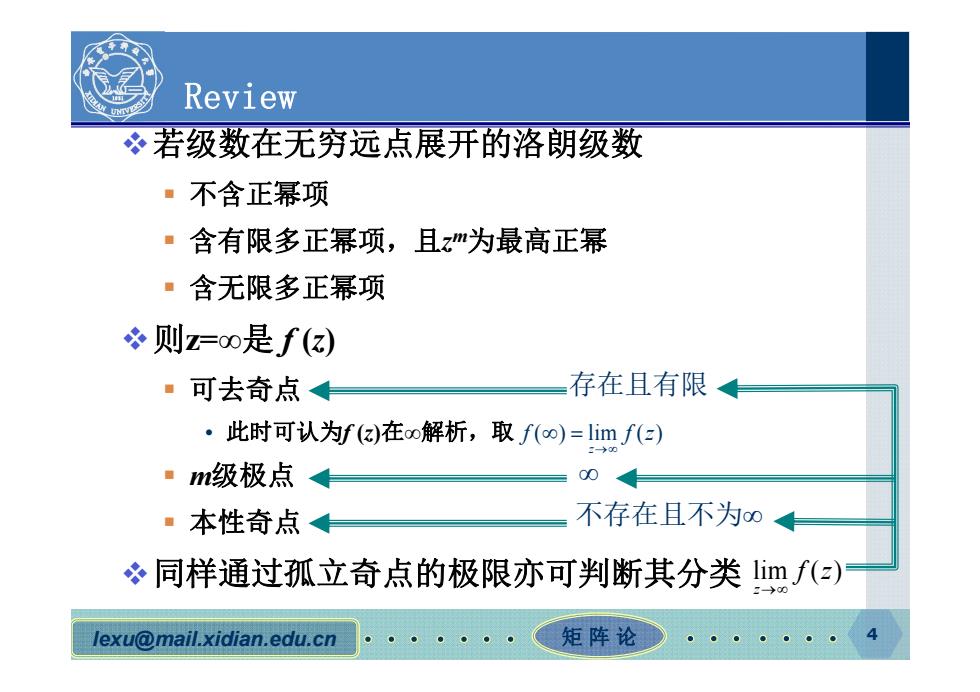
Review 若级数在无穷远点展开的洛朗级数 ·不含正幂项 ·含有限多正幂项,且zm为最高正幂 ·含无限多正幂项 则z=o是f() ·可去奇点《 存在且有限 ·此时可认为f)在oo解析,取f(o)=limf(a) m级极点 004 ·本性奇点 不存在且不为0 同样通过孤立奇点的极限亦可判断其分类limf(z) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 4 Review 若级数在无穷远点展开的洛朗级数 不含正幂项 含有限多正幂项,且zm为最高正幂 含无限多正幂项 则z=∞是 f (z) 可去奇点 • 此时可认为f (z)在∞解析,取 m级极点 本性奇点 同样通过孤立奇点的极限亦可判断其分类 lim ( ) z f z 存在且有限 ∞ 不存在且不为∞ ( ) lim ( ) z f f z

第20讲留数 留数及留数定理 留数计算 在无穷远点的留数 留数在定积分中的应用(① lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 5 第20讲 留数 留数及留数定理 留数计算 在无穷远点的留数 留数在定积分中的应用(I)