
Jordan标准形 ·多项式矩阵的初等变换 ·初等变换的目的是为了在保持矩阵原有属性 的前提下形式上变得简单 1.互换两行(列) 2.以非零常数乘以某行(列) ·这里不能乘以的多项式或零,这样有可能改变原来矩阵 的秩和属性 3.将某行(列)乘以的多项式加到另一行(列) lexu@mail.xidian.edu.cn 矩阵论 6
lexu@mail.xidian.edu.cn 矩 阵 论 6 Jordan标准形 多项式矩阵的初等变换 初等变换的目的是为了在保持矩阵原有属性 的前提下形式上变得简单 1. 互换两行(列) 2. 以非零常数乘以某行(列) 这里不能乘以λ的多项式或零,这样有可能改变原来矩阵 的秩和属性 3. 将某行(列)乘以λ的多项式加到另一行(列)
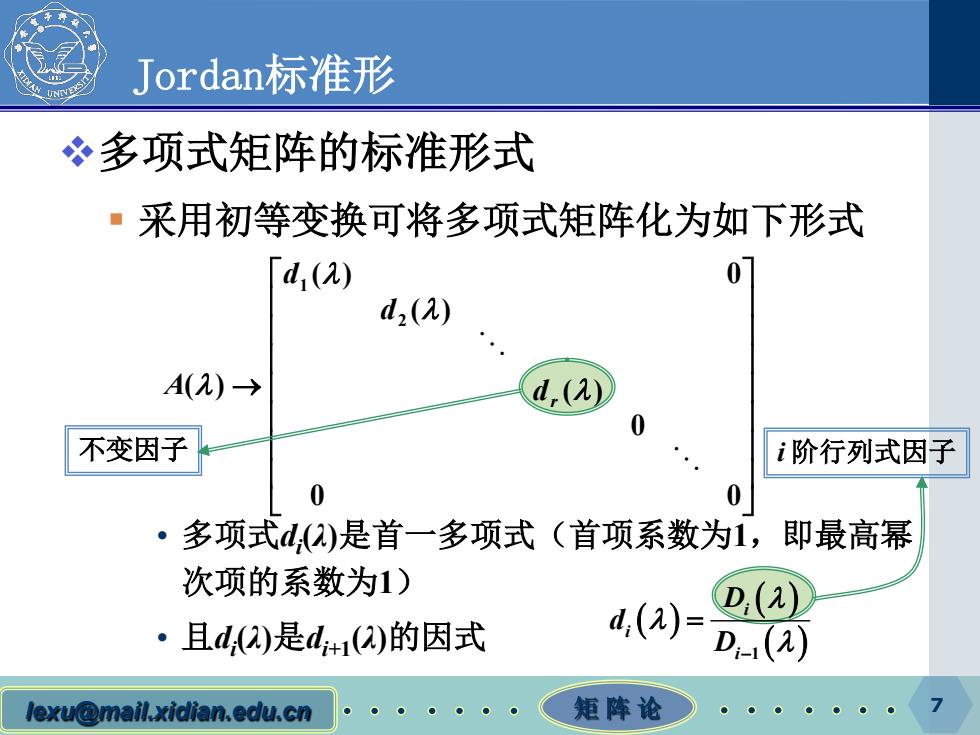
Jordan标准形 冬多项式矩阵的标准形式 ■采用初等变换可将多项式矩阵化为如下形式 d(2) d2(2) A(2)→ d,(2) 不变因子 i阶行列式因子 0 0 。 多项式d()是首一多项式(首项系数为1,即最高幂 次项的系数为1) D(2 ·且d以(2)是d+1(2)的因式 d,()- D-(2) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 7 Jordan标准形 多项式矩阵的标准形式 采用初等变换可将多项式矩阵化为如下形式 • 多项式di (λ)是首一多项式(首项系数为1,即最高幂 次项的系数为1) • 且di (λ)是di+1(λ)的因式 → 0 0 0 ( ) ( ) ( ) 0 ( ) 2 1 λ λ λ λ r d d d A ( ) ( ) ( ) 1 i i i D d D λ λ − λ = 不变因子 i 阶行列式因子

Jordan标准形 Jordan标准形的求法 ·求出特征矩阵(I-A)的初等因子组 (-元)m(2-)、、(2-2,)m ·写出各Jordan块矩阵(一个初等因子对应一个 Jordan:块矩阵) 「21 0 (2-2)m→J(2)= 0 lexu@mail.xidian.edu.cn 矩阵论 ●●● 8
lexu@mail.xidian.edu.cn 矩 阵 论 8 Jordan标准形 Jordan标准形的求法 求出特征矩阵(λI - A)的初等因子组 写出各Jordan块矩阵(一个初等因子对应一个 Jordan块矩阵) ( ) 1 1 m λ λ − ( ) () × −→ = 1 0 1 0 i i i i m i i ii i m m J λ λ λλ λ λ

Jordan标准形 冬Jordan标准形的求法 "合成Jordan矩阵 0 J2 J= lexu@mail.xidian.edu.cn 矩阵论 9
lexu@mail.xidian.edu.cn 矩 阵 论 9 Jordan标准形 Jordan标准形的求法 合成Jordan矩阵 = s J J J J 0 0 2 1

第7进Jordan标准形分析 Jordan标准形求解 Jordan标准形变换矩阵求解 lexu@mail.xidian.edu.cn 矩阵论 10
lexu@mail.xidian.edu.cn 矩 阵 论 10 第7讲 Jordan标准形分析 Jordan标准形求解(II) Jordan标准形变换矩阵求解