
1931 矩阵论 主讲教师:徐乐 2014年10月29日星期三
2014年10月29日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 第四讲线性变换矩阵及其对角化 ■线性变换的矩阵表示 ·线性变换及矩阵的值域和核 ·特征值和特征向量 ·矩阵对角化的充要条件 lexu@mail.xidian.edu.cn 矩阵论 。。。·。。。2
lexu@mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第四 讲 线性变换矩阵及其对角化 线性变换的矩阵表示 线性变换及矩阵的值域和核 特征值和特征向量 矩阵对角化的充要条件
线性变换的矩阵表示 线性变换用矩阵表示,将抽象的线性变换转化为 具体的矩阵形式 ·设T是线性空间V"的一个线性变换 51 。{x1,x2,…,xn}是V"的的一个基 x=[x1,x2,…,Xn 52 x∈Vm,存在唯一的坐标表示 51 5 52 X←> Tx=[T(x,2,…,xn)】 =[x,x,…,x]A TxA 把A称为在基化1,x2,…,xn}下的矩阵 lexu@mail.xidian.edu.cn 矩阵论 ● 3
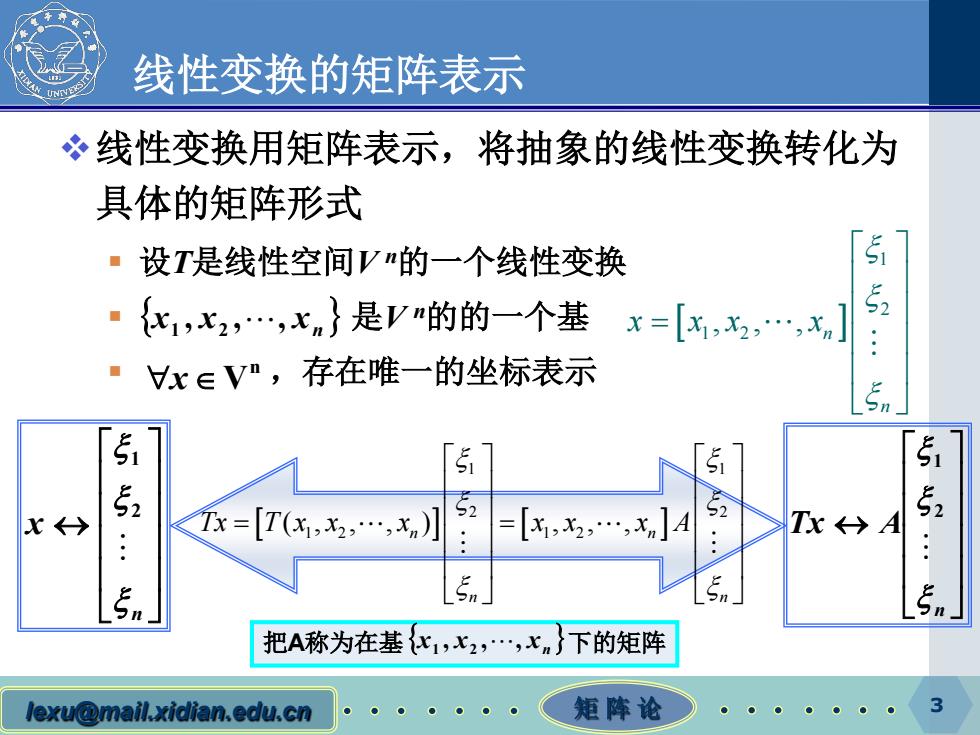
lexu@mail.xidian.edu.cn 矩 阵 论 3 线性变换的矩阵表示 线性变换用矩阵表示,将抽象的线性变换转化为 具体的矩阵形式 设T是线性空间V n的一个线性变换 是V n的的一个基 ,存在唯一的坐标表示 {x1 , x2 ,, xn } n ∀ ∈x V [ ] 1 2 1 2 ,,, n n x xx x ξ ξ ξ = [ ] [ ] 1 1 2 2 1 2 1 2 (, , , ) , , , n n n n Tx T x x x x x x A ξ ξ ξ ξ ξ ξ = = ↔ n x ξ ξ ξ 2 1 ↔ n Tx A ξ ξ ξ 2 1 把A称为在基 {x1 , x2 ,, xn }下的矩阵

线性变换的矩阵表示 冬相似矩阵 ■设T在V的两个基的矩阵分别为A和B {1,x2,…,xn} {i,x2,…,xn} ·且ki,,,x]=k,,,xn则 B=C-AC ·即A和B为相似矩阵 冬定理 ·n阶方阵A和B相似的充要条件是A和B为同一线 性变换在不同基下的矩阵 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 4 线性变换的矩阵表示 相似矩阵 设T在V n的两个基的矩阵分别为A和B 且 则 即A和B为相似矩阵 定理 n阶方阵A和B相似的充要条件是A和B为同一线 性变换在不同基下的矩阵 {x1 , x2 ,, xn } { } ' ' 2 ' 1 , , , x x xn [x , x , , xn ] [x1 , x2 , , xn ]C ' ' 2 ' 1 = 1 B C AC − =

线性变换及矩阵的值域和核 冬定义 ■设T是线性空间V"的线性变换,称 R(T)={xxeV}为T的值域 dim R(T) ·N(T)={x|x∈V",Ix=0}为T的核 dim NT) 『的秩和零度 ■R(T和N(T均为Vn的子空间 设A为mXn阶矩阵,称 ·R(A)={Ax|x∈R"orx∈C"} 为矩阵4A的值域 ·N(A)={xlx∈R"or x∈C,Ax=0为矩阵A的核 dim R(A) dim N(A) A的秩和零度 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 5 线性变换及矩阵的值域和核 定义 设T是线性空间V n的线性变换,称 • 为T的值域 • 为T的核 R(T)和N(T)均为V n的子空间 设A为m×n阶矩阵,称 • 为矩阵A的值域 • 为矩阵A的核 { }n R T Tx x () | V = ∈ { } n N T x x Tx ( ) | V, 0 =∈ = { } n n R A Ax x x ( ) | R or C =∈ ∈ { } n n N A x x x Ax ( ) | R or C , 0 =∈ ∈ = dim R(T) dim N(T) dim R(A) dim N(A) T的秩和零度 A的秩和零度