西安电子科技大学：《矩阵论》研究生课程教学课件（讲义，2014）14 矩阵的奇异值分解

131 UNIVE 矩阵论 主讲教师：徐乐 2014年12月10日星期三

2014年12月10日星期三 矩 阵 论 主讲教师：徐乐

不红 上讲回顾 第13讲QR分解及满秩分解 ·矩阵QR分解计算方法 ·矩阵的满秩分解 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第13讲 QR分解及满秩分解  矩阵QR分解计算方法  矩阵的满秩分解

QR分解 冬求QR分解的方法 ·方法一l采用Givens,方法 ■方法二]采用Householde方法 ·[方法三]Gram-schmidt正交归一化方法 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 QR分解 求QR分解的方法  [方法一]采用Givens方法  [方法二]采用Householde方法  [方法三] Gram-schmidt正交归一化方法

矩阵的满秩分解 冬定义 E∈Cmxr,G1 ECrxn ■设A∈Cmx"(r>0) =FGL ·若存在矩阵F∈CIXr G∈Crx =(FD)(D-G) ·使得A=FG =F(DD-)G ·称其为A的一个满秩分解 A=FG ■Note: ·F为列满秩矩阵，即列数等于秩 VD∈Crw ·G为行满秩矩阵，即行数等于秩 任何非零矩阵均 ·满秩分解不唯一 可逆方阵 存在满秩矩阵 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 矩阵的满秩分解 定义  设 • 若存在矩阵 • 使得A=FG • 称其为A的一个满秩分解  Note： • F为列满秩矩阵，即列数等于秩 • G为行满秩矩阵，即行数等于秩 • 满秩分解不唯一 m n A C (r 0) r    m r F Cr   r n G Cr  r r D Cr   可逆方阵 1 1 1 1 F G (FD)(D G) F(DD )G A FG       mr rn F C ,G C 1r 1r     任何非零矩阵均 存在满秩矩阵

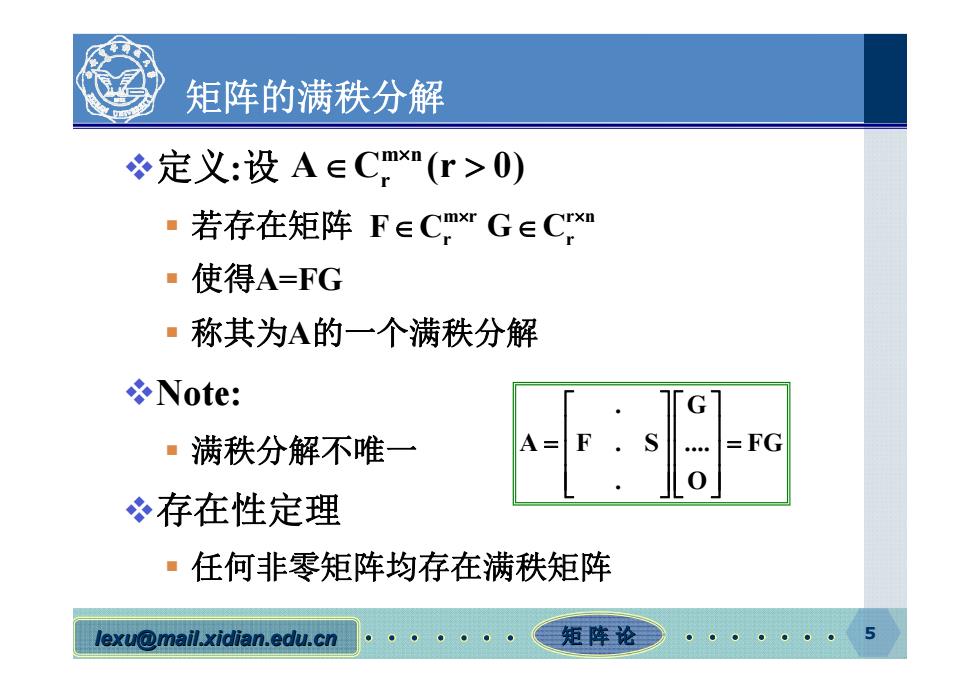
矩阵的满秩分解 定义：设A∈Cmx"(r>0) ·若存在矩阵F∈CIrG∈Cxn ■使得A=FG ·称其为A的一个满秩分解 Note: G ·满秩分解不唯一 =FG 0 冬存在性定理 ·任何非零矩阵均存在满秩矩阵 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 矩阵的满秩分解 定义:设  若存在矩阵  使得A=FG  称其为A的一个满秩分解 Note:  满秩分解不唯一 存在性定理  任何非零矩阵均存在满秩矩阵 m n A C (r 0) r    m r F Cr   r n G Cr  . G A F . S .... FG . O                 