
SIT 复变函数与场论 主讲:徐乐
复变函数与场论 主讲:徐乐
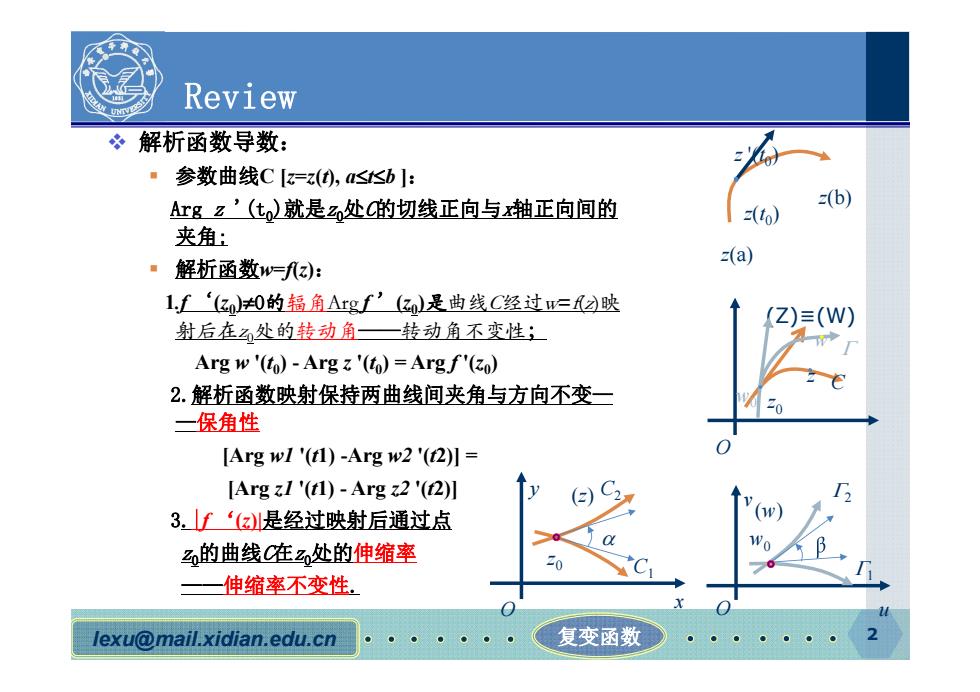
Review 解析函数导数: 参数曲线C[=z④,a≤≤b: Argz’(t就是处C的切线正向与轴正向间的 (b) (to) 夹角: (a) 解析函数w=孔): L,f‘(k00的辐角Arg’(z是曲线C经过w=映 Z)≡(W) 射后在处的转动角—转动角不变性; Arg w'(to)-Arg z'(to)=Argf'(zo) 2.解析函数映射保持两曲线间夹角与方向不变一 一保角性 [Arg wI'(t1)-Arg w2'(t2)]= [Arg zI'(t1)-Arg 22'(12)] 3.f‘是经过映射后通过点 的曲线C在处的伸缩率 一伸缩率不变性 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 2 O Review 解析函数导数: 参数曲线C [z=z(t), atb ]: Arg z '(t0)就是z0处C的切线正向与x轴正向间的 夹角; 解析函数w=f(z): 1.f ‘(z0)0的辐角Arg f ’(z0)是曲线C经过w=f(z)映 射后在z 0处的转动角——转动角不变性; Arg w '(t0) - Arg z '(t0) = Arg f '(z0) 2.解析函数映射保持两曲线间夹角与方向不变— —保角性 [Arg w1 '(t1) -Arg w2 '(t2)] = [Arg z1 '(t1) - Arg z2 '(t2)] 3.|f ‘(z)|是经过映射后通过点 z0的曲线C在z0处的伸缩率 ——伸缩率不变性. z(a) z(b) z(t0) z '(t0) z0 z C w0 (Z)≡(W) w y O (z) z0 C1 C2 x v O u (w) w0 1 2
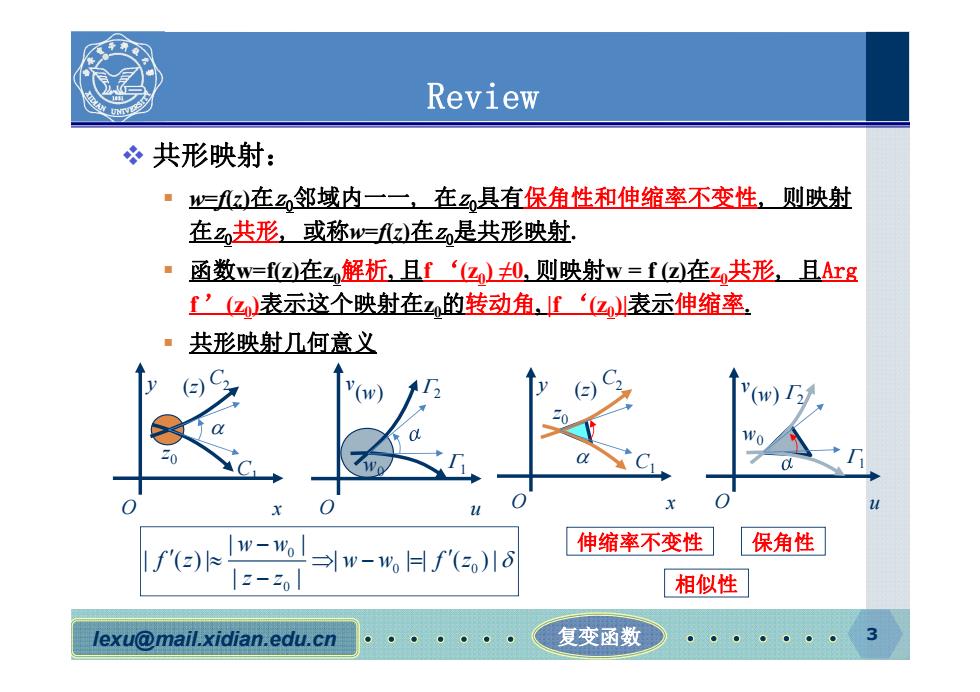
Review 冬共形映射: =fz在邻域内一一在Z,具有保角性和伸缩率不变性,则映射 在2共形,或称w=☑在是共形映射; 函数w=f☑在Z解析.且f‘亿0.则映射w=f☑在2共形,且Arg f’(亿表示这个映射在2的转动角.f‘亿表示伸缩率 共形映射几何意义 f'(z) w=ww-w,日f'(5)1ò 伸缩率不变性 保角性 相似性 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 3 O x y (z) z0 C1 C2 O u v(w) w0 1 2 O x y O u (z) v(w) z0 w0 C1 C2 1 2 共形映射: w=f(z)在z0邻域内一一, 在z0具有保角性和伸缩率不变性, 则映射 在z0共形, 或称w=f(z)在z0是共形映射. 函数w=f(z)在z0解析, 且f ‘(z0) ≠0, 则映射w = f (z)在z0共形, 且Arg f ’(z0)表示这个映射在z0的转动角, |f ‘(z0)|表示伸缩率. 共形映射几何意义 Review 0 0 0 0 | | | ( ) | | || ( ) | | | w w fz ww fz z z 伸缩率不变性 保角性 相似性

Review 冬分式线形映射 az+b a b ·逆射仍为分式线形映射; w= cz+d cd →ad-bct0 ·复合仍为分式线形映射; ■三类特殊分式线形映射: 平移 i )w=z+b 旋转+伸缩 ii )w=az 反演变换 iii)w=1/z ·扩充复平面上一一对应,且具有以下性质 D具有保角性; D具有保圆性; D具有保对称性; lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 4 Review 分式线形映射 逆射仍为分式线形映射; 复合仍为分式线形映射; 三类特殊分式线形映射: 扩充复平面上一一对应,且具有以下性质 具有保角性; 具有保圆性; 具有保对称性; 0 az b a b w ad bc cz d c d i ) ii ) iii) 1/ w zb w az w z 平移 旋转+伸缩 反演变换
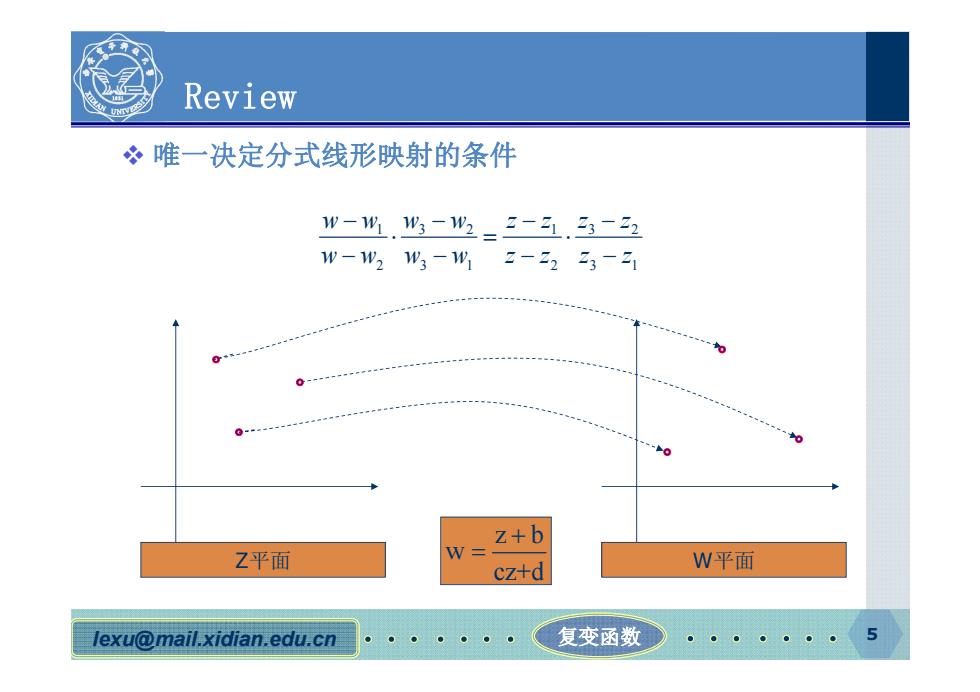
Review 冬唯一决定分式线形映射的条件 w-w.w3-w2=2-.3-22 w-w2%3-"2-2223-21 x--- z+b Z平面 W= cz+d W平面 lexu@mail.xidian.edu.cn 复变函数 5
lexu@mail.xidian.edu.cn 复变函数 5 Review 唯一决定分式线形映射的条件 Z平面 W平面 z b w cz+d 1 1 3 2 32 2 3 1 23 1 ww zz ww zz ww w w zz z z