电子科技大学：《数值分析 Numerical Analysis》课程教学资源（课件讲稿）矩阵特征值与特征向量的计算

算法4.1 1.输入A,初始向量x,误差限8，最大迭代次数N; 2.置k=l,元=ma(e好y=元 3.计算x=,B=max(x,y= 4.若2-<6，输出B,y,停机；否则，转5 5.若k<N,置k=k+1,2=B,转3，否则输出 失败信息，停机. 11

11 2. 1, max( ); ; x k  x y  置    1. 输入 A, 初始向量 x, 误差限  , 最大迭代次数 N; 3. , max( ), ; x x Ay  x y  计算    4. 若      , 输出  , y, 停机; 否则, 转5; 5. , 1, , 3 , , . 若 k  N 置k  k     转 否则输出 失败信息 停机

幂法适用范围： 求大型稀疏矩阵按模最大的特征值入，· 矩阵的特征值分布为，2，>2m+之…之2n 2为单根或重根，即入=…2m, 矩阵有n个线性无关的特征向量. 12

12 1 求大型稀疏矩阵按模最大的特征值 . 1 1 , 矩阵的特征值分布为    m      n 1 1 m  为单根或重根, 即  , 矩阵有n个线性无关的特征向量

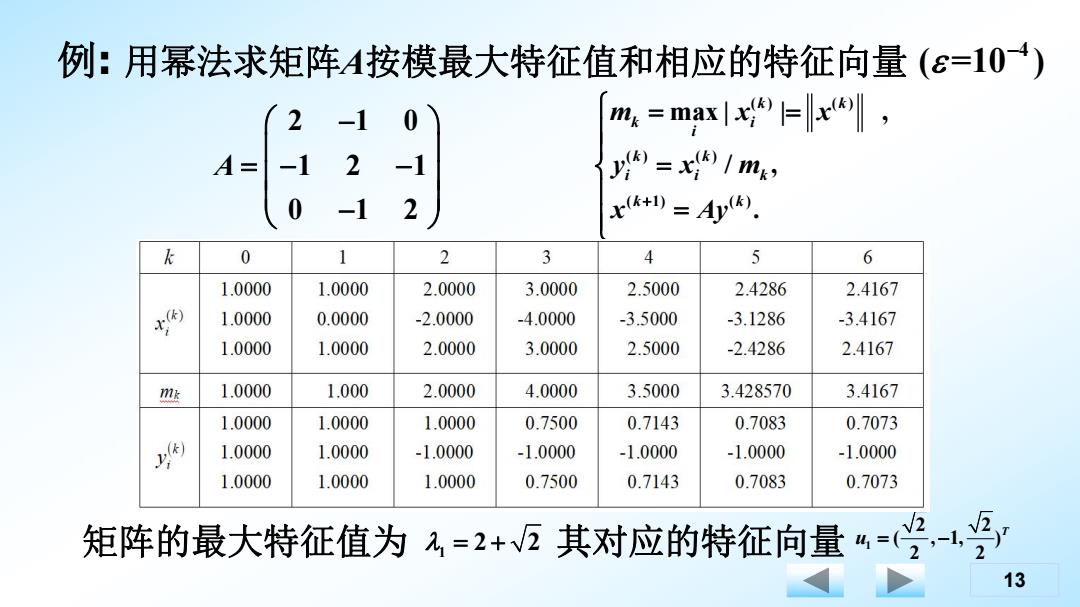
例：用幂法求矩阵A按模最大特征值和相应的特征向量（ε=104） 2 m=maxlx(, A= -1 2 -1 y)=x(/mg> 0 -1 2 x+w=. k 0 2 3 4 5 6 1.0000 1.0000 2.0000 3.0000 2.5000 2.4286 2.4167 1.0000 0.0000 -2.0000 -4.0000 -3.5000 -3.1286 -3.4167 1.0000 1.0000 2.0000 3.0000 2.5000 -2.4286 2.4167 me 1.0000 1.000 2.0000 4.0000 3.5000 3.428570 3.4167 1.0000 1.0000 1.0000 0.7500 0.7143 0.7083 0.7073 1.0000 1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 1.0000 1.0000 1.0000 0.7500 0.7143 0.7083 0.7073 矩阵的最大特征值为元-2+2其对应的特征向量4-受号 13

13 例: 用幂法求矩阵A按模最大特征值和相应的特征向量 2 1 0 1 2 1 0 1 2 A            ( ) ( ) ( ) ( ) ( 1) ( ) max | | , / , . k k k i i k k i i k k k m x x y x m x Ay           矩阵的最大特征值为 1  2  2 其对应的特征向量 1 2 2 ( , 1, ) 2 2 T u   4 ( =10 ) 

幂法的收敛速度取决于比值r= 比值越小，收敛越快 1.2幂法的加速 (一)原点移位法 2,是A的特征值，则2：-。是A-2I的特征值 x(k+1)=(A-A)x(5) =-a+会会a+经安a 14

14 2 1 , , .   幂法的收敛速度取决于比值 r= 比值越小 收敛越快 1.2 幂法的加速 （一）原点移位法 i A i 0 A 0  是 的特征值，则    是   I 的特征值 ( 1) ( ) 0 1 2 0 1 0 1 1 0 1 2 2 1 0 1 0 ( ) ( ) [ ( ) ( ) ] k k k k n k 1 n n x A I x u u u                             

设A有特征值元，且21>22>…，取1使得 闪->3-且 8 2,-2o 用幂法求A-2I的按模最大的特征值1，则几1=21+九， 这种方法称为原点移位法。 注：实际应用时，A的特征值不知道，无法确定，当收敛 速度慢时，可以适当移动原点 15

15 1 2 0 , , 设 A 有 特 征 值  i 且      取  使 得 1 0  i 0 0 1 2 1 0 1 m a x i i           且 * 0 1 1 1 0 A  I     ,  用幂法求  的按模最大的特征值 , 则   这种方法称为原点移位法. 注：实际应用时，A的特征值不知道， 无法确定，当收敛 速度慢时, 可以适当移动原点. 