
1.0 1.0 0.5 例:计算矩阵A= 1.0 1.0 0.25 按模取最大的特征值 0.5 0.25 2.0 k y因=xmax) ≈max() 0 (1,1,1) 先用规范化的幂法计算: (0.9091, 0.8182, 1 2.75 19 (0.7482, 0.6497,1)y 2.5365374 20 (0.7482,0.6497, 1)y 2.5365323 采用原点位移的加速法求解,取=0.75,矩阵B=A-,I y内=xmax(x) ≈max() 0 (1,1,1) 9 (0.7483,0.6497,1) 1.7866587 10 (0.7483,0.6497,1) 1.7865914 由以上两表得到:1=41+2≈2.5365914 16
16 1.0 1.0 0.5 1.0 1.0 0.25 0.5 0.25 2.0 A 例:计算矩阵 按模取最大的特征值 采用原点位移的加速法求解,取 λ0 = 0.75, 矩阵 B = A - λ0I 1 1 0 由以上两表得到: 2.5365914 先用规范化的幂法计算:
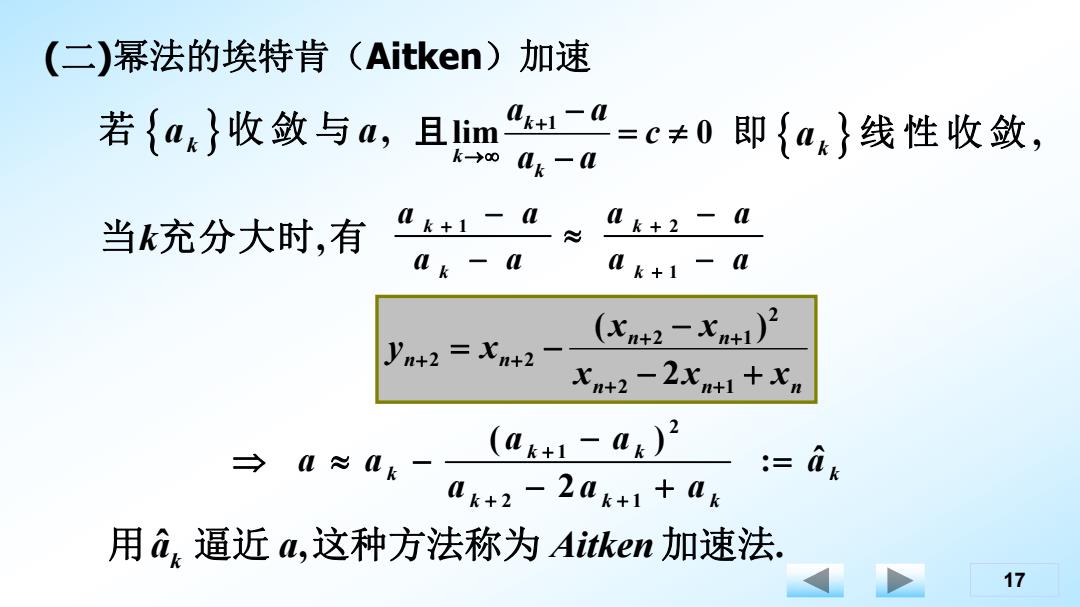
(二)幂法的埃特肯(Aitken)加速 若{a4}收敛与a,且1im"一a=c≠0即{a}线性收敛, k→oLk-0 当k充分大时,有 0k+1 0k+2-0 0k- 0k+1-0 (xn+2-xn+1)2 ym2=Xm2m2-2ma → (ak+1-ak)2 :-ax ak+2-20k+1+0k 用d,逼近a,这种方法称为Aitken加速法. 17
17 (二)幂法的埃特肯(Aitken)加速 , k 若 a 收 敛 与 a 1 lim 0 k k k a a c a a 且 , k 即 a 线 性 收 敛 当k充分大时,有 1 2 1 k k k k a a a a a a a a 2 1 2 1 ( ) 2 k k k k k k a a a a a a a ˆ , . k 用a 逼近 a 这种方法称为 Aitken 加速法 : ˆ k a n n n n n n n x x x x x y x 2 1 2 2 1 2 2 2 ( )

算法4.2 1.输入A=(a),初始向量x,误差限6,最大迭代次数N, 2.置k=1,a=0,a,=0,=1.0,y=maxx) X 3.计算x=Ay,置max(x)→x2, x max(x) →Jy, (a1-a)2 4.计算元=a,-2a+0, 5.若2-<,输出元,y停机,否则转6, 6.若k<N,置→,0,=4,九→,k+1→k转3,否则,输出 失败信息停机 18
18 1. ( ), , , , A ij 输入 a 初始向量x 误差限 最大迭代次数N 0 1 0 2. 1, 0, 0, 1.0, , max( ) x k y x 置 2 3. , max( ) , , max( ) x x Ay x y x 计算 置 0 5. 若 , 输出, y 停机,否则转6, 1 0 2 1 0 6. , , , , 1 , 3, , , . 若k N 置 k k 转 否则 输出 失败信息 停机 2 1 0 0 2 1 0 ( ) 4. , 2 计算

(三)对称矩阵的Rayleigh商加速法 x"Ax ·定义:设A对称,x≠0,则称R(x)= x7x 为x关于A的 Rayleigh商。 R())=( 1 (Axx 19
19 (三) 对称矩阵的Rayleigh商加速法 • 定义: 设A对称,x 0,则称 为 x 关于A的 Rayleigh商。 ( ) T T x Ax R x x x 2 2 1 2 (0) 1 (0) ( ) 1 2 (0) (0) 1 2 2 1 1 ( ) ( ) ( ) n k k k T k j j k j k T k n k j j j A x A x R y O A x A x

p)= x() Ax(o) max(x())max(4x()) ·公式 tw=小=n4 max(x()) 称为Rayleigh ,-g- 商加速法。 此外 R)→元,y→业 max(v) 20
20 • 公式 称为Rayleigh 商加速法。 ( ) ( ) 1 1 1 ( ) , max( ) k k v R y y v ( ) (0) ( ) ( ) (0) 1 (0) ( 1) ( ) (0) ( ) ( ) (0) 1 (0) ( ) ( ) ( ) (0) (0) max( ) max( ) max( ) ( ) ( ) ( ) ( ) ( ) ( ) k k k k k k k k k k T k k T k k k T k k T k x A x y x A x A x x Ay A x y Ay A x A x R y y y A x A x 此外