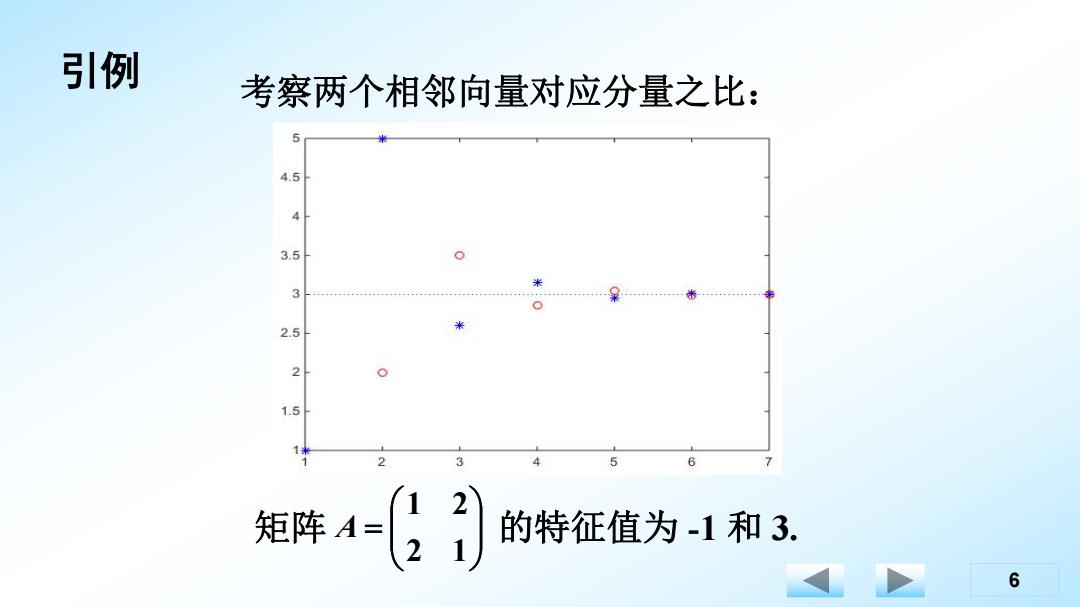
引例 考察两个相邻向量对应分量之比: 4.5 3.5 0 米 3 2.5 米 2 1.5 2 5 6 矩阵A= 的特征值为-1和3. 6
6 考察两个相邻向量对应分量之比: 矩阵 的特征值为 -1 和 3. 2 1 1 2 A 引例

§1 幂法和反幂法 1.1幂法 用于求矩阵的按模最大的特征值与相应的特征向量的近似值。 设A为n阶实矩阵,2,w,(i=1,2,…,n)为A的特征值 和相应的特征向量, 且满足:2>2≥23≥…≥2 1,山2,…,Wn,线性无关. 7
7 1.1 幂法 用于求矩阵的按模最大的特征值与相应的特征向量的近似值。 , , ( 1, 2, , ) A n i ui 设 为 阶实矩阵 i n 为 A的特征值 和相应的特征向量, 1 2 3 n 且满足: 1 2 , , , , . u u un 线性无关 §1 幂法和反幂法

对任意向量x), 有xo=∑a,W,a,不全为零. =1 x(k+1) x=A+1x0) = 4“aw=2a% i=1 +安r…字小] ≈2+'a, 8
8 , 1 (0 ) n i iui 有x (k 1) (k ) x Ax 1 1 1 1 k u 1 1 n k i i i i u k 1 (0) A x ( 0 ) x 不全为零 . i 1 1 n k i i i A u 1 2 1 1 1 1 1 2 2 1 1 ( ) ( ) k k n k u n n a u a u 对任意向量

定理:设A∈Rx",特征值九,(i=1,2,…n)满足 >2≥2g≥…≥2, 且与2对应的特征向量4,42,…4n线性无关,则对任意 非零初始向量x(a,≠0),向量序列 xk)=Ax0)-→2&, 西→k→0. 相应的特征向量为xk+). 注:x+≈2+a,W1,实际计算时将xk+)标准化。 9
9 1 2 3 1 2 (0) 1 ( 1) ( ) (0) 1 1 1 ( ) 1 , ( 1, 2, ) , , , ( 0), ( ). n n i n i n k k k k i k i A R i n u u u x x x A x u k x 定理:设 特征值 满足 且与 对应的特征向量 线性无关,则对任意 非零初始向量 向量序列 , ( 1) 1 ( 1) 1 1 1 k k k x u x 注: ,实际计算时将 标准化。 ( 1) . k x 相应的特征向量为

标准化 设与入,对应的特征向量 u 若心=(化,…x,h七,卡2七记七=ma() 取初始向量x,将x标准化为y x(k)=Ay(k-1) max(x)’k=1,2,… 则y)→ maG' max(x)-→,(k→o) 10
10 ( ) ( 1) ( ) ( ) ( ) , 1, 2, max( ) k k k k k x Ay x y k x ( ) 1 ( ) 1 1 , m ax( ) ( ) m ax( ) k u k y x k u 则 (0) (0) (0) 取初始向量 x ,将 x 标准化为 y 设与1对应的特征向量 u1 1 2 1 ( , , ), | | max(| |), max( ) n r i r i n x x x x x x x x 若 记