
5.什么是超几何分布? 提示:一般地,若有总数为N件的甲、乙两类物品,其中甲类有 M件(M<N),从所有物品中随机取出n件(n≤N),则这n件中所含 甲类物品数X是一个离散型随机变量,X能取不小于t且不大于 s的所有自然数,其中s是M与n中的较小者,t在n不大于乙类物 品件数(即n≤N-M0时取0,否则t取n减乙类物品件数之差(即 t=n-(N-M0),而且PX=k)= CC CN ,k=t,什1,…S,这里的X称为服 从参数为N,n,M的超几何分布,记作X~HN,n,M)
导航 5.什么是超几何分布? 提示:一般地,若有总数为N件的甲、乙两类物品,其中甲类有 M件(M<N),从所有物品中随机取出n件(n≤N),则这n件中所含 甲类物品数X是一个离散型随机变量,X能取不小于t且不大于 s的所有自然数,其中s是M与n中的较小者,t在n不大于乙类物 品件数(即n≤N-M)时取0,否则t取n减乙类物品件数之差(即 t=n-(N-M)),而且P(X=k)= ,k=t,t+1,…,s,这里的X称为服 从参数为N,n,M的超几何分布,记作X~H(N,n,M). 𝐂 𝑴 𝒌 𝐂𝑵-𝑴 𝒏-𝒌 𝐂𝑵 𝒏

6.什么是离散型随机变量的均值和方差? 提示:(1)均值:一般地,如果离散型随机变量X的分布列如下表 所示. X 1 X2 ●●● Xk ●●● n P p 卫k ●●● Pn n 则称EP+P2+t比Pn=∑xp:为离散型随机变量X的 1三1 均值或数学期望(简称期望).离散型随机变量X的均值E)也 可用EX表示,它刻画了X的平均取值
导航 6.什么是离散型随机变量的均值和方差? 提示:(1)均值:一般地,如果离散型随机变量X的分布列如下表 所示. X x1 x2 … xk … xn P p1 p2 … pk … pn 则称E(X)=x1p1+x2p2+…+xnpn= 为离散型随机变量X的 均值或数学期望(简称期望).离散型随机变量X的均值E(X)也 可用EX表示,它刻画了X的平均取值. ∑ 𝒊=𝟏 𝒏 xipi
导航 (2)方差:设离散型随机变量X的分布列为 X x1 X2 XR ●●0 水n P Pk ●●● Pn n 因为X的均值为E),所以DX)=∑K,E()IP;能够刻画X相 i=1 对于均值的离散程度(或波动大小),这称为离散型随机变量X 的方差
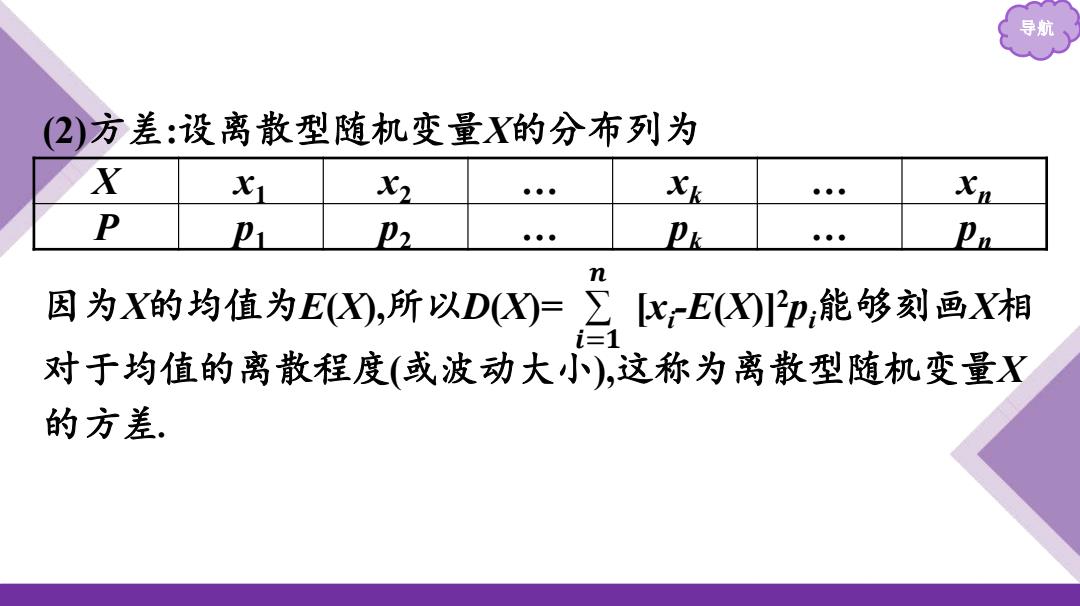
导航 (2)方差:设离散型随机变量X的分布列为 X x1 x2 … xk … xn P p1 p2 … pk … pn 因为X的均值为E(X),所以D(X)= [xi -E(X)]2pi能够刻画X相 对于均值的离散程度(或波动大小),这称为离散型随机变量X 的方差. ∑ 𝒊=𝟏 𝒏

导加 7.几种特殊分布的均值和方差分别是什么? 提示:(1)若X服从参数为p的两点分布,则EX)=p,DX)=p(1-p) (2)若X~B(np),则E(X)=np,D(X凶=np(1-p), (S)若X~HN,n,M,则E)nM 8.均值和方差有什么性质? 提示:若X与Y都是随机变量,且Y=X+b(0),则 E(Y)=E(aX+b)=aE(X)+b,D(Y)=D(aX+b)=a2D(X)
导航 7.几种特殊分布的均值和方差分别是什么? 提示:(1)若X服从参数为p的两点分布,则E(X)=p,D(X)=p(1-p). (2)若X~B(n,p),则E(X)=np,D(X)=np(1-p). (3)若 X~H(N,n,M),则 8.均值和方差有什么性质? 提示:若X与Y都是随机变量,且Y=aX+b(a≠0),则 E(Y)=E(aX+b)=aE(X)+b,D(Y)=D(aX+b)=a2D(X). E(X)= 𝒏𝑴 𝑵

导 9.正态曲线有什么性质? 提示:(1)正态曲线关于直线x=对称(即决定正态曲线对称轴 的位置),具有中间高、两边低的特点; (2)正态曲线与x轴所围成的图形面积为1; (3)σ决定正态曲线的“胖瘦”:σ越大,说明标准差越大,数据的 集中程度越弱,所以曲线越“胖”,σ越小,说明标准差越小,数据 的集中程度越强,所以曲线越“瘦
导航 9.正态曲线有什么性质? 提示:(1)正态曲线关于直线x=μ对称(即μ决定正态曲线对称轴 的位置),具有中间高、两边低的特点; (2)正态曲线与x轴所围成的图形面积为1; (3)σ决定正态曲线的“胖瘦”:σ越大,说明标准差越大,数据的 集中程度越弱,所以曲线越“胖”,σ越小,说明标准差越小,数据 的集中程度越强,所以曲线越“瘦”