
全程设计 复习课 第2课时 概率与统计
复习课 第2课时 概率与统计

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破
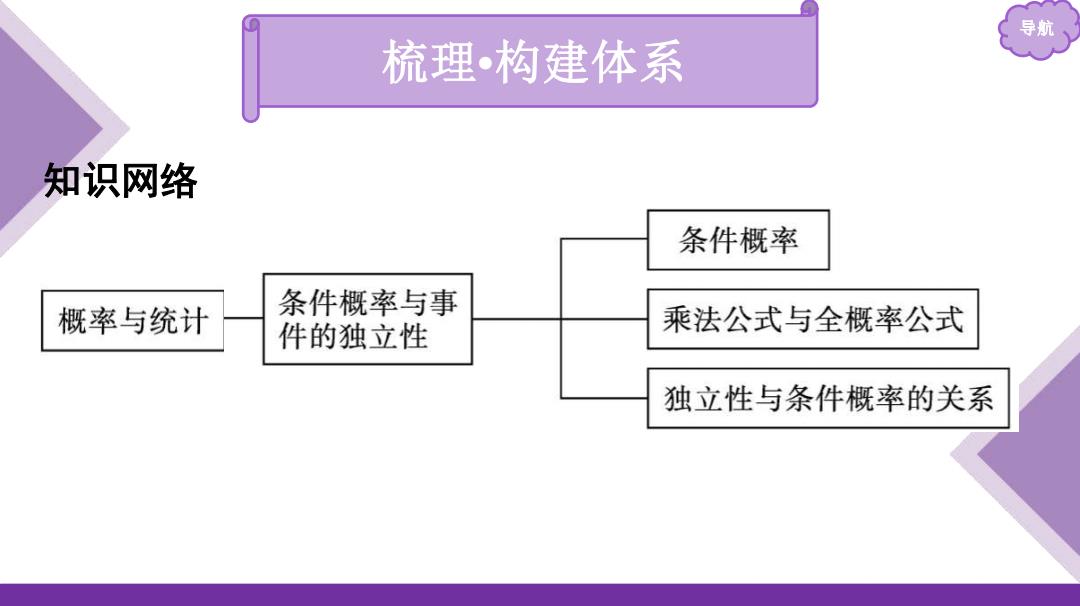
导航 梳理构建体系 知识网络 条件概率 概率与统计 条件概率与事 件的独立性 乘法公式与全概率公式 独立性与条件概率的关系
导航 梳理 •构建体系 知识网 络
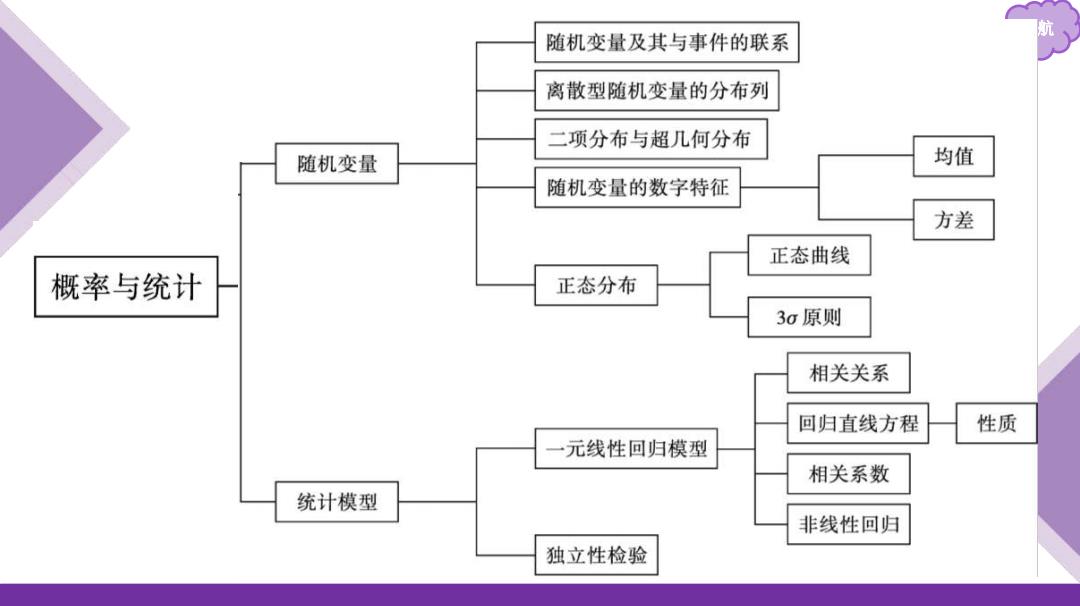
随机变量及其与事件的联系 离散型随机变量的分布列 二项分布与超几何分布 随机变量 均值 随机变量的数字特征 方差 正态曲线 概率与统计 正态分布 30原则 相关关系 回归直线方程 性质 元线性回归模型 相关系数 统计模型 非线性回归 独立性检验
导航

导期 要点梳理 1.条件概率的概念是什么?具有什么性质? 提示:(1)一般地,当事件B发生的概率大于0时(即P(B)>0),已知 事件B发生的条件下事件A发生的概率,称为条件概率,记作 P4B,而且PAB)=PAn8 P(B) (2)假设A,B,C都是事件,且P(A>0,根据条件概率的定义,可得 ①0≤P(BA)1;②P(AA)=1;③如果B与C互斥,则 P((BUC)A)=P(BA)+P(CA)
导航 要点梳理 1.条件概率的概念是什么?具有什么性质? 提示:(1)一般地,当事件B发生的概率大于0时(即P(B)>0),已知 事件B发生的条件下事件A发生的概率,称为条件概率,记作 P(A|B),而且P(A|B) = (2)假设A,B,C都是事件,且P(A)>0,根据条件概率的定义,可得 ①0≤P(B|A)≤1;②P(A|A) =1;③如果B与C互斥,则 P((B∪C)|A)=P(B|A)+P(C|A). 𝑷(𝑨⋂𝑩) 𝑷(𝑩)