
线性方程狙的直接解法1 ·高斯消去法 ·列主元消去法 ·LU分解
线性方程组的直接解法1 • 高斯消去法 • 列主元消去法 • LU分解

线性方程组的直接解法1 ·高斯消去法 ·列主元消去法 ·LU分解
线性方程组的直接解法1 • 高斯消去法 • 列主元消去法 • LU分解
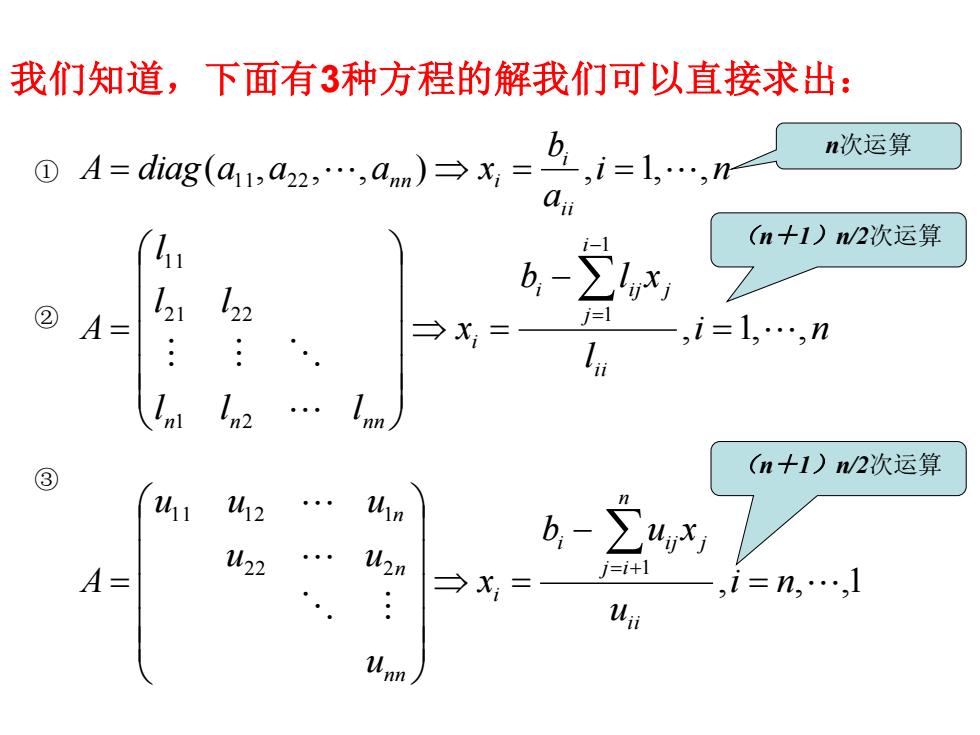
我们知道,下面有3种方程的解我们可以直接求出: 0=加g(aa,a)→x=,=lm n次运算 0 1- (n+1)/2次运算 ②A i=1 →X= -,i=1,.,n nn ⊙ (n十1)n/2次运算 212 6-∑4,x 1W22 u2n →X= j=i+1 ,i=n,.,1 u
我们知道,下面有3种方程的解我们可以直接求出: i n a b A diag a a a x i i i n n i ( , , , ) , 1, , ① = 1 1 2 2 = = n次运算 i n l b l x x l l l l l l A i i i j i i j j i n n n n , 1, , 1 1 1 2 2 1 2 2 1 1 = − = = − ② = (n+1)n/2次运算 , , ,1 2 2 2 1 1 1 1 2 1 i n u b u x x u u u u u u A i i n j i i i j j i n n n n = − = = = + ③ (n+1)n/2次运算

对线性方程组作如下的变换,解不变: ①交换两个方程的次序 ②一个方程的两边同时乘以一个非0的数 ③一个方程的两边同时乘以一个非0数,加到另一个方程 因此,增广矩阵A,b)作如下的变换,方程组的解不变 ①交换矩阵的两行 ②某一行乘以一个非0的数 ③某一个乘以一个非0数,加到另一行 消元法就是对增广矩阵作上述行的变换,变为我们已 知的3种类型之一,而后求根
对线性方程组作如下的变换,解不变: ①交换两个方程的次序 ②一个方程的两边同时乘以一个非0的数 ③一个方程的两边同时乘以一个非0数,加到另一个方程 因此,增广矩阵(A,b) 作如下的变换,方程组的解不变 ①交换矩阵的两行 ②某一行乘以一个非0的数 ③某一个乘以一个非0数,加到另一行 消元法就是对增广矩阵作上述行的变换,变为我们已 知的3种类型之一,而后求根
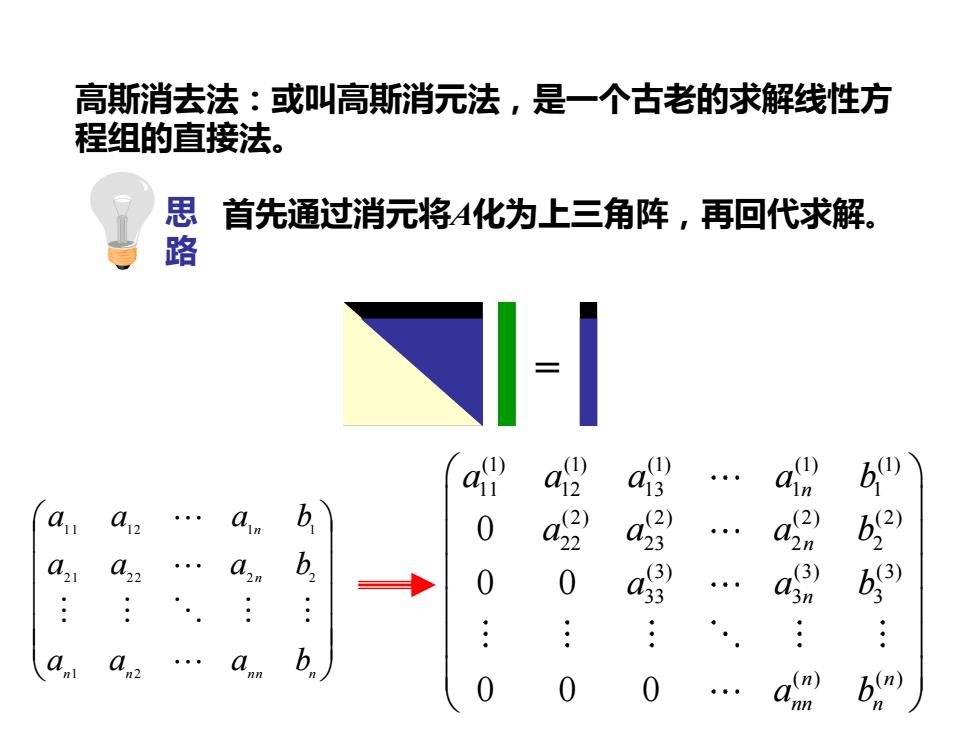
高斯消去法:或叫高斯消元法,是一个古老的求解线性方 程组的直接法。 思首先通过消元将4化为上三角阵,再回代求解 路 a a 0 a a12 . 0 a品 b2 a2 22 02m 0 0 a a a a,2 b 0 0 0 b
高斯消去法:或叫高斯消元法,是一个古老的求解线性方 程组的直接法。 n n n n n n n a a a b a a a b a a a b 1 2 2 1 2 2 2 2 1 1 1 2 1 1 (1) (1) (1) (1) (1) 11 12 13 1 1 (2) (2) (2) (2) 22 23 2 2 (3) (3) (3) 33 3 3 ( ) ( ) 0 0 0 0 0 0 n n n n n nn n a a a a b a a a b a a b a b 思 路 首先通过消元将A化为上三角阵,再回代求解。 =