
主要内容 ·高斯求积公式的定义 ·高斯求积公式的构造 ·数值微分与误差估计
主要内容 • 高斯求积公式的定义 • 高斯求积公式的构造 • 数值微分与误差估计

插值型求积公式的 最高代数精度讨论 [f(x)k≈∑Af(x) 前面讨论求积公式构造的过程中,节点x(k=0,1, 2,.,)是确定的,而且通常情况下是等距分布的。 对于一个两节点的插值求积公式,待求的求积系数个 数为2。一般情况下,如果求积公式具有1次代数精度, 则所有求积系数可通过方程式求解如下例: 试确定一个具有1次代数精度的公式 〔f(x)d=Af(a)+Af(b)
插值型求积公式的 最高代数精度讨论 = n i k k b a f x dx A f x 0 ( ) ( ) 前面讨论求积公式构造的过程中,节点xk (k=0,1, 2, . ,n)是确定的,而且通常情况下是等距分布的。 对于一个两节点的插值求积公式,待求的求积系数个 数为2。一般情况下,如果求积公式具有1次代数精度, 则所有求积系数可通过方程式求解.如下例: 试确定一个具有1次代数精度的公式 ( ) ( ) ( ) f x dx A0 f a A1 f b b a = +

试确定一个具有1次代数精度的公式 f(x)≈Af(a)+Af(b) 解:因为当(i=0,1)时,∫xd分别为(b-a)和(b-a) 故要公式具有1次代数精度,则必须有 f(x)=1 [Af(a)+Af(b)=A+A=b-a f(x)=x Af(a)+Af(b)=aA+bA=(b-a) 解此方程组得:A,=A= b-a 梯形公式 求积公式 rxw=i,fa+fol
试确定一个具有1次代数精度的公式 解:因为当 故要公式具有1次代数精度,则必须有 f (x) = 1 f (x) = x ( ) ( ) ( ) f x dx A0 f a A1 f b b a + 时, 分别为 和 ( ), 2 1 ( 0,1) ( ) 2 2 i x dx b a b a b a i = − − + = + = − + = + = − ( ) 2 1 ( ) ( ) ( ) ( ) 2 2 0 1 0 1 0 1 0 1 A f a A f b aA bA b a A f a A f b A A b a 解此方程组得: 2 0 1 b a A A − = = ( ) ( ) 2 求积 式 ( ) f a f b b a f x dx b a + − 公 梯形公式

求积公式∫(x)d≈Af(a)+Af(b)要具有2次精度,则必须满足 f(x)=1A+A=b-a f(x)=xaA+bA =(b2-a)/2 f(x)=x aA+bA=(b-a)/3 两个变量 三个独立方程 将人=4=6,2代入最后一个方程的左边,符到 “(+6)≠,4→以上方程组为“不盾方程组巴 2 3 如果假设求积节点可以任意选择,即求积公式) 四个变量 三个独立方程 f(x)d=Af(x,)+Af(xb则以上方程变为 还需补充一个方程 A∫(x)+A∫(x)=A,+A=b-a Af(x)+Af(x,)=xA+x,A=(bi-a)/2 Af(x)+Af(x,)=x4+xA=(bi-a)/3
f (x) = 1 f (x) = x 求积公式 f (x)dx A0 f (a) A1 f (b)要具有2次精度,则必须满足 b a + + = − + = − + = − ( )/ 3 ( )/ 2 3 3 1 2 0 2 2 2 0 1 0 1 a A b A b a aA bA b a A A b a 2 f (x) = x 3 ( ) 2 3 3 2 2 b a a b b a − + − 将 代入最后一个方程的左边,得到 2 0 1 b a A A − = = 以上方程组为“矛盾方程组” 两个变量 三个独立方程 ,则以上方程变为 如果假设求积节点可以任意选择,即求积公式为 ( ) ( ) ( ) 0 0 1 1 f x dx A f x A f x b a = + + = + = − + = + = − + = + = − ( ) ( ) ( )/ 3 ( ) ( ) ( )/ 2 ( ) ( ) 3 3 1 2 0 1 2 0 0 1 1 0 2 2 0 0 1 1 0 0 1 1 0 0 1 1 0 1 A f x A f x x A x A b a A f x A f x x A x A b a A f x A f x A A b a 四个变量 三个独立方程 还需补充一个方程
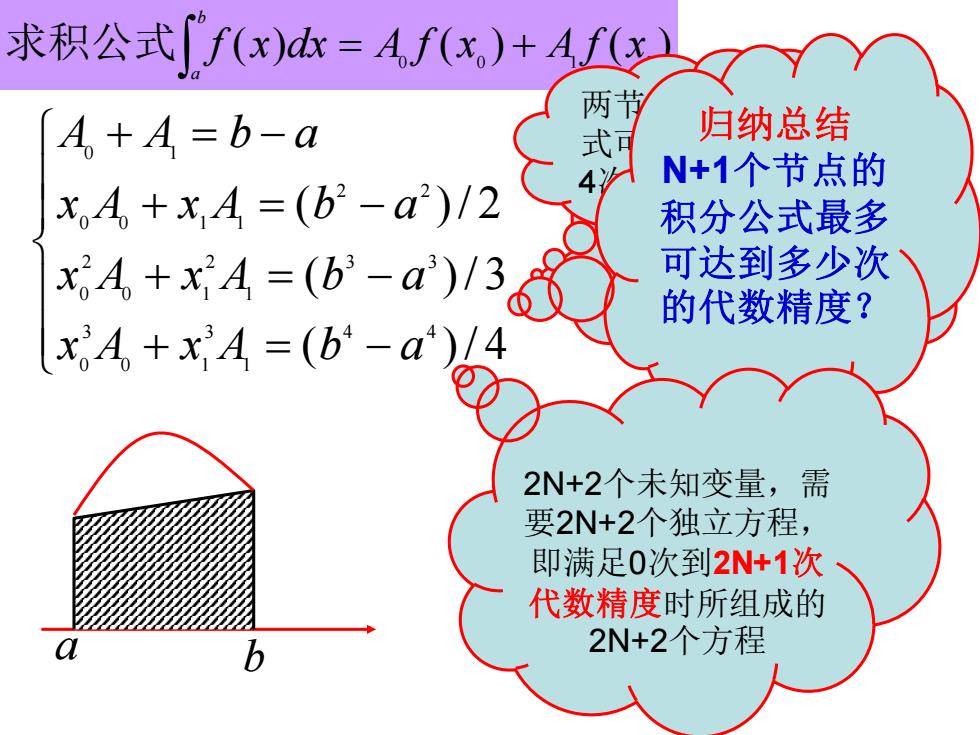
求积公式f(x)=Af(x)+Af(x 两节 A+4=b-a 式可 归纳总结 N+1个节点的 x4+x,A=(b2-a2)/2 4 积分公式最多 xA+x4=(b-a)1365 可达到多少次 的代数精度? xiA+xA=(bi-a)/4 2N+2个未知变量,需 要2N+2个独立方程, 即满足0次到2N+1次 代数精度时所组成的 2N+2个方程
( ) ( ) ( ) 0 0 1 1 f x dx A f x A f x b a = + 求积公式 + = − + = − + = − + = − ( )/ 4 ( )/ 3 ( )/ 2 4 4 1 3 0 1 3 0 3 3 1 2 0 1 2 0 2 2 0 0 1 1 0 1 x A x A b a x A x A b a x A x A b a A A b a 四个变量 四个独立方程 最终得到的求积公 式具有3次代数精度 两节点求积公 式可不可能有 4次代数精度? a b a 0 b x 1 x 归纳总结 N+1个节点的 积分公式最多 可达到多少次 的代数精度? 2N+2个未知变量,需 要2N+2个独立方程, 即满足0次到2N+1次 代数精度时所组成的 2N+2个方程