
线性方程徂的直接解法1 ·对称正定阵的分解定理 ·对称正定阵的分解公式 ·平方根法及改进的平方根法 ·三对角线性方程组的追赶法
线性方程组的直接解法1 • 对称正定阵的分解定理 • 对称正定阵的分解公式 • 平方根法及改进的平方根法 • 三对角线性方程组的追赶法

线性方程狙的直接解法巴 ·对称正定阵的分解定理 ·对称正定阵的分解公式 ·平方根法及改进的平方根法 ·三对角线性方程组的追赶法
线性方程组的直接解法2 • 对称正定阵的分解定理 • 对称正定阵的分解公式 • 平方根法及改进的平方根法 • 三对角线性方程组的追赶法

定理2.1(用紧凑格式解线性方程组的充分条件) 如果阶方阵A的各阶顺序主子式不为零,即 a,≠0, 0,.4≠0, a22 则方阵A必可作LU分解,且分解是唯一的。 定理2.2: 如果A为n阶对称方阵,且A的各阶顺序 主子式都不为零,则A可唯一分解为 A-LDL 其中L为单位下三角阵,D为对角阵
定理2.1(用紧凑格式解线性方程组的充分条件) 则方阵 必可作 分解,且分解是唯一的。 如果 阶方阵 的各阶顺序主子式不为零,即 A LU A a a a a a 0, 0, , 0, n A 2 1 2 2 1 1 1 2 1 1 定理2.2: 其中 为单位下三角阵, 为对角阵。 主子式都不为零,则 可唯一分解为 如果 为 阶对称方阵,且 的各阶顺序 D A LDL A A A T L n =
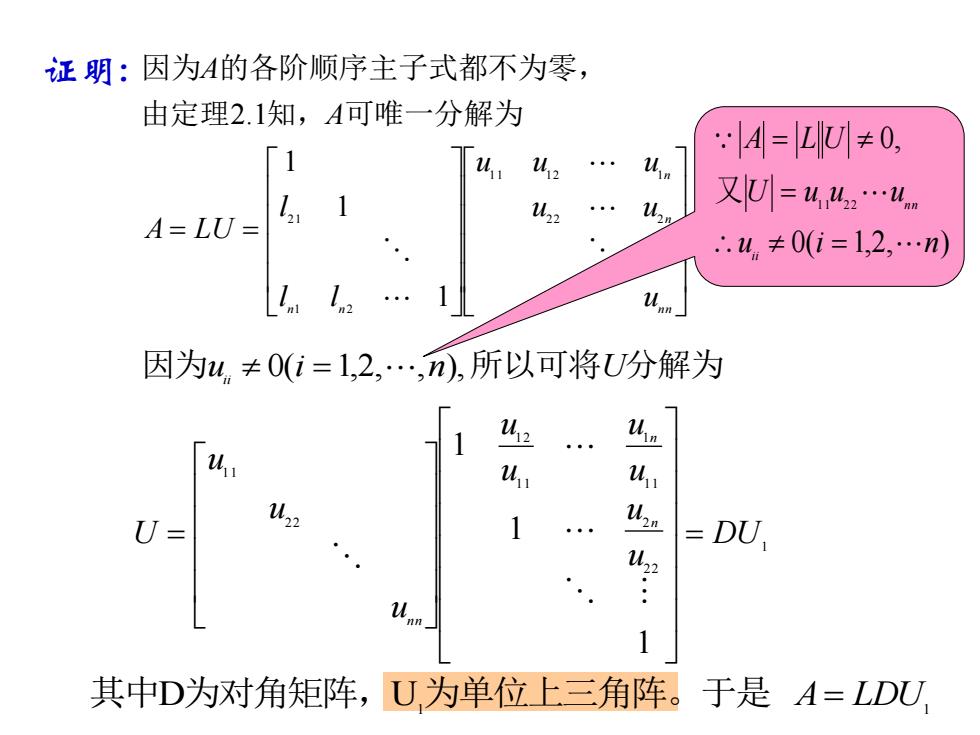
证明:因为A的各阶顺序主子式都不为零, 由定理2.1知,A可唯一分解为 1 4=LU≠0, u u, 又U=442.un A=LU= .u.≠0(i=1,2,.n) 1. 因为4.≠0(i=1,2,.,n),所以可将U分解为 2 DU 其中D为对角矩阵,U为单位上三角阵。于是A=LDU
= = n n n n n n u u u u u u l l l A LU A A 2 2 2 1 1 1 2 1 1 2 2 1 1 1 1 由定理2.1知, 可唯一分解为 证明: 因为 的各阶顺序主子式都不为零, 因为uii 0(i =1,2, ,n),所以可将U分解为 0( 1,2, ) 0, 1 1 2 2 u i n U u u u A L U ii n n = = = 又 其中D为对角矩阵,U1 为单位上三角阵。于是 A= LDU1 1 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 1 DU u u u u u u u u u U n n n n = =
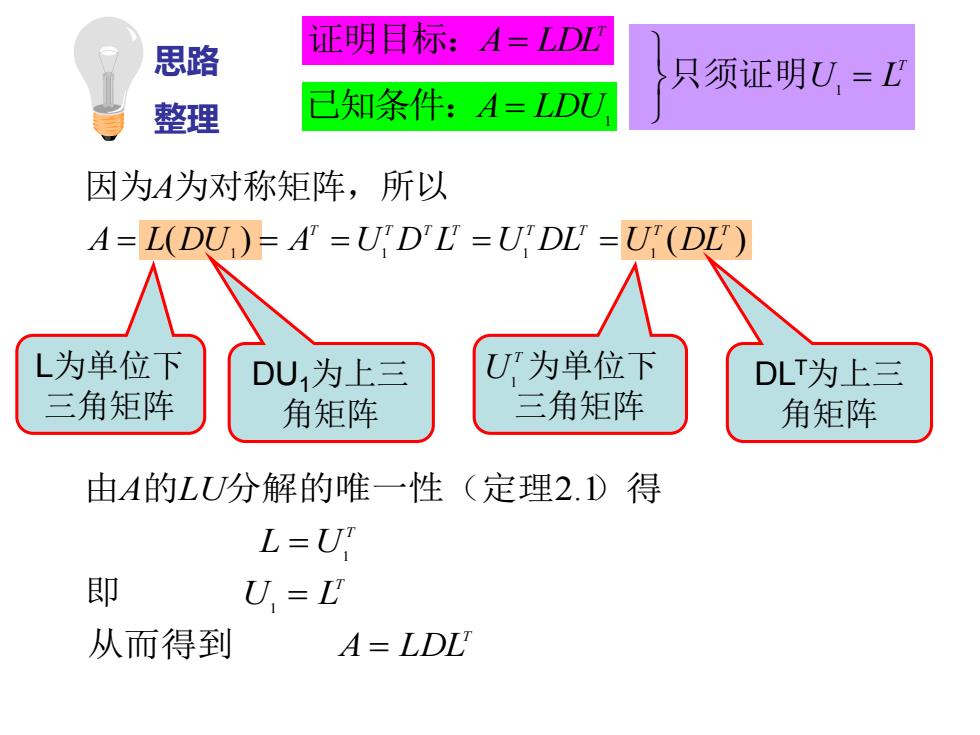
思路 证明目标:A=LDL 只须证明U= 整理 已知条件:A=LDU 因为A为对称矩阵,所以 A=L(DU )=A=UD'L=UDL =U(DL) L为单位下 DU1为上三 U”为单位下 DLT为上三 三角矩阵 角矩阵 三角矩阵 角矩阵 由A的LU分解的唯一性(定理2.D得 L=U' 即 U=L 从而得到 A-LDL
为单位下 三角矩阵 T U1 DLT为上三 角矩阵 L为单位下 三角矩阵 DU1为上三 角矩阵 ( ) ( ) 1 1 1 1 T T T T T T T T A L DU A U D L U DL U DL A = = = = = 因为 为对称矩阵,所以 T T T A LDL U L L U A LU = = = 从而得到 即 由 的 分解的唯一性(定理 )得 1 1 2.1 已知条件:A= LDU1 T 证明目标:A= LDL T U = L 只须证明 1 思路 整理