
数据插值 ·差商的概念 ·牛顿插值多项式构造 。 牛顿插值多项式误差分析 。 差分的概念 ·等距节点插值公式
数据插值 • 差商的概念 • 牛顿插值多项式构造 • 牛顿插值多项式误差分析 • 差分的概念 • 等距节点插值公式

49=立- (x-x) P.(x)=4,xy 0 当你写程序时,你会发觉Lagrange 插值多项式是很容易计算的
噢是吗? 如果现在的 插值不够精确呢 那么你也许想取更多的节点 ? . 对. 那么所有的 Lagrange 基函数, l i (x), 都要重新计算. 很好 ! 我们现在介绍差商的概念, 并讨论解决这个问题方法. 当你写程序时, 你会发觉Lagrange 插值多项式是很容易计算的. = − − = n j j i i j j i x x x x l x 0 ( ) ( ) ( ) 0 ( ) ( ) n n i i i P x l x y = =
§4.3差商与差分及其性质 定义4.3.1差商(亦称均差) f(x:)-f(x) 称为f关于x,和x的 jx,≠xj) 两者相同 1阶差商 ≠ 2阶差商 Xi-XK 两者相同 (k+1)阶差商: f1,.,x+l=ff,l Xo一Xk+1
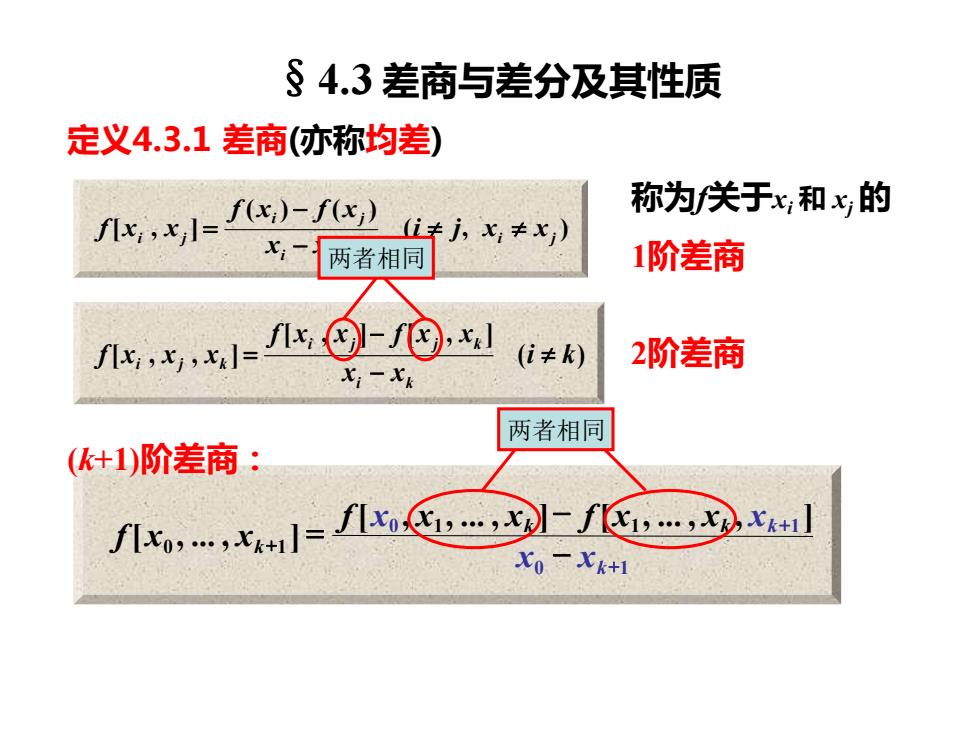
定义4.3.1 差商(亦称均差) ( , ) ( ) ( ) [ , ] i j i j i j i j i j x x x x f x f x f x x − − = 称为f关于xi 和 xj 的 1阶差商 ( ) [ , ] [ , ] [ , , ] i k x x f x x f x x f x x x i k i j j k i j k − − = 2阶差商 §4.3 差商与差分及其性质 0 1 0 1 1 1 0 1 [ , , . , ] [ , . , , ] [ , . , ] + + + − − = k k k k k x x f x x x f x x x f x x (k+1)阶差商: 两者相同 两者相同

差商的对称性 差商[X,X1,X2,.,X]可以随意改变结点次序,而差商值不变 -阶差商:fx,x]=x)-f)-f)-f-x,x1 X。-x X-X。 二阶差商: -fxx] X。一X2 fx.-xx:-fx X2-X。 X2-X
差商的对称性 差商f[x0 ,x1 ,x2 ,.,xn ]可以随意改变结点次序,而差商值不变. 一阶差商: [ , ] ( ) ( ) ( ) ( ) [ , ] 1 0 1 0 1 0 0 1 0 1 0 1 f x x x x f x f x x x f x f x f x x = − − = − − = 二阶差商: [ , , ] [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] [ , , ] 2 1 0 2 0 2 1 1 0 2 0 1 2 0 1 0 2 0 1 1 2 0 1 2 f x x x x x f x x f x x x x f x x f x x x x f x x f x x f x x x = − − = − − = − − =

f(x)-f(x,)f(x)-f(x,) f[xo,X.X,J=- x-X2 X。-X1 X2-Xo xf(x)-xf(x)+xf(x)-xf(x,)+xf(x,)-x:f(x) (x-x2)(x。-x)(x2-x) f(x)-f(x,)f(x)-f(x2) f[x,x,x2]= X-X。 X。一X, x-x, %f(x)-xf(x)+xf(x,)-xf(x,)+xf(x)-xf(x,) (x,-x2)(x。-x(x2-xo) 其他情况大家可以仿照以上过程自行证明
( )( )( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ , , ] 1 2 0 1 2 0 0 2 0 1 1 0 1 2 2 1 2 0 2 0 0 1 0 1 1 2 1 2 0 1 2 x x x x x x x f x x f x x f x x f x x f x x f x x x x x f x f x x x f x f x f x x x − − − − + − + − = − − − − − − = ( )( )( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ , , ] 1 2 0 1 2 0 0 2 0 1 1 0 1 2 2 1 2 0 1 2 0 2 0 2 1 0 1 0 1 0 2 x x x x x x x f x x f x x f x x f x x f x x f x x x x x f x f x x x f x f x f x x x − − − − + − + − = − − − − − − = 其他情况大家可以仿照以上过程自行证明