
主要内容 ·数值积分的意义 ·插值积分公式的构造 ·插值积分公式的精度 ·龙贝格积分公式
主要内容 • 数值积分的意义 • 插值积分公式的构造 • 插值积分公式的精度 • 龙贝格积分公式

为什么要数值积分? 在微积分里,按Newton-Leibniz公式 求定积分 要求被积函数f(x) © 有解析表达式: F(x)有解析表达式 ©f(x)的原函数F(x)为初等函数
在微积分里,按Newton-Leibniz公式 求定积分 要求被积函数f(x) ☞ 有解析表达式; ☞ f(x)的原函数F(x)为初等函数. 为什么要数值积分? F(x)有解析表达式

问题 f(x)没有解析表达式,只有数表形式 e.g. X 1 2 3 4 5 f(x) 4 4.5 6 8 8.5 f(x)有表达式,但原函数不是初等函数 (arctanx/x 它们的原函数都不是初等函数
问题 f(x)没有解析表达式,只有数表形式 e.g. x 1 2 3 4 5 f(x) 4 4.5 6 8 8.5 f(x)有表达式,但原函数不是初等函数 e.g. , 它们的原函数都不是初等函数。 1 2 0 x e dx − 1 0 (arctan ) x x dx

求定积分就得通过近似计算一数值积分求得 积分近似值。 基本思想: 是对被积函数进行近似,给出数值积分,同 时考虑近似精度 可采用数据插 值方法获得(x) 的近似函数
求定积分就得通过近似计算-数值积分求得 积分近似值。 基本思想: 是对被积函数进行近似,给出数值积分,同 时考虑近似精度。 可采用数据插 值方法获得f(x) 的近似函数
设在区) 数值积分就是将定积分计 <x =b, 由n+] 算简化为计算被积函数在 直多项式有 各节点处函数值的线性组 值点 合。求积系数的确定以及 求积公式的误差分析成为 (常量) 数值积分研究的主要内容。 dx 品-0 @(x) kfx)=∑Af(x) k=0 插值求积公式, 由插值节点决定, Ak为求积系数 与f(x无关,记为Ak (可事先求出)
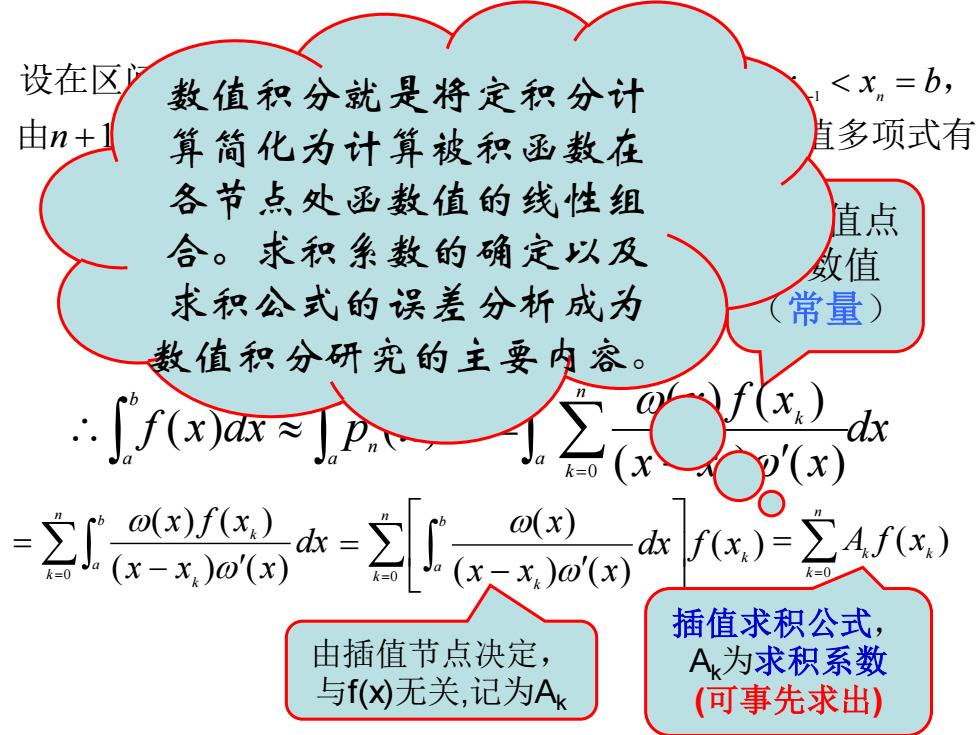
由 个数据点( 作一插值多项式有 设在区间 上有 个节点 , 1 , ( )) ( 0,1,2, , ) [ , ] 1 0 1 2 1 n x f x k n a b n a x x x x x b k k n n + = + = − = = − = n k k k k n x x x x p x 0 ( ) ( ) ( ) ( ) 各插值点 函数值 (常量) = − = b a n k k k b a n b a n dx x x x x f x f x dx p x dx p x f x 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − = n k b a k k dx x x x x f x 0 ( ) ( ) ( ) ( ) = − = n k k b a k dx f x x x x x 0 ( ) ( ) ( ) ( ) = = n k k k A f x 0 ( ) 由插值节点决定, 与f(x)无关,记为Ak 插值求积公式, Ak为求积系数 (可事先求出) 数值积分就是将定积分计 算简化为计算被积函数在 各节点处函数值的线性组 合。求积系数的确定以及 求积公式的误差分析成为 数值积分研究的主要内容