
主要内容 ·阿达姆斯(Adams)公式 ·一阶微分方程组求解 ·高阶微分方程求解
主要内容 • 阿达姆斯(Adams)公式 • 一阶微分方程组求解 • 高阶微分方程求解
问题提出: 前面所讲的微分方程求解方法中,在计算y+1时都只 用到前面所得的一个值即y,如果能够多利用前面 已算出的y,.,y等多个值的信息,可能会 提高计算的精确度。阿达姆斯(Adams)方法就是 0次插值对应 1次插值对应 高次插值推出 于矩形公式求 于梯形公式求 阿达姆斯公式 积,推出欧拉 上 积,推出梯形 (分为内插、 方法 是 法则 外插) yn+1 -y dt y P(tdt
问题提出: 前面所讲的微分方程求解方法中,在计算yn+1时都只 用到前面所得的一个值即yn,如果能够多利用前面 已算出的y0, y1,., yn等多个值的信息,可能会 提高计算的精确度。阿达姆斯(Adams)方法就是 基于这种设想的一种线性多步法(用到前面多步的 数值结果)。 y P t dt y y f t y t dt x n x n n x n x n n n + + + = + = + 1 1 1 ( ) ( , ( )) 或 的构造形式是决定微分方程求解方法的主要因素 。 从数值计算原理上讲, 或 的插值多项式 ( ) ( , ) ( , ( )) ( ) P t f x y f t y t P x 0次插值对应 于矩形公式求 积,推出欧拉 方法 1次插值对应 于梯形公式求 积,推出梯形 法则 高次插值推出 阿达姆斯公式 (分为内插、 外插)
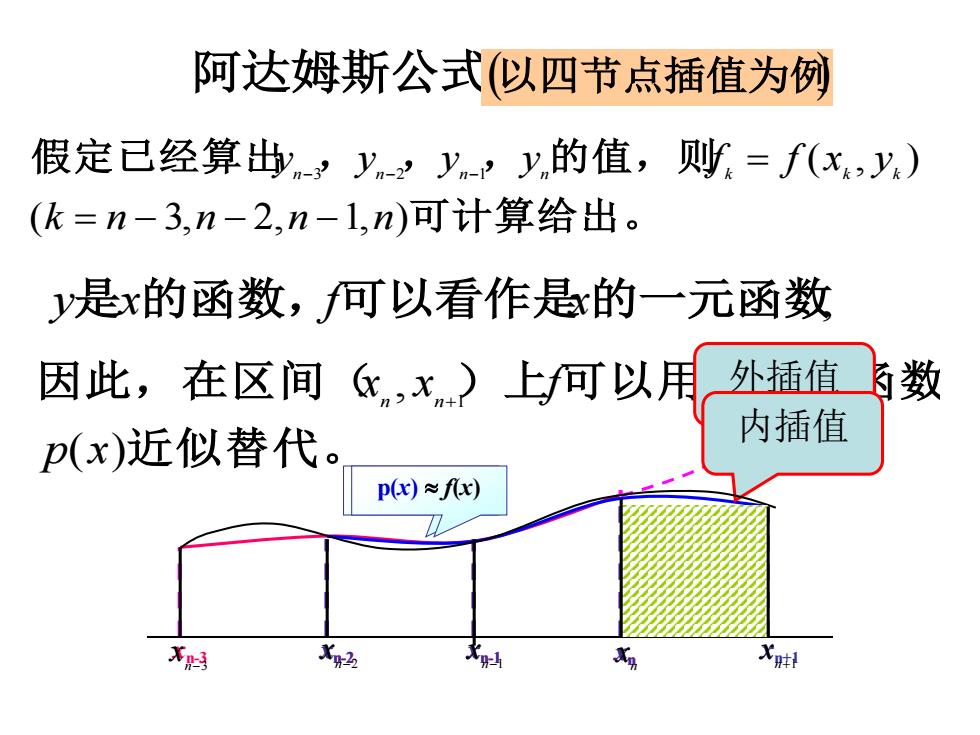
阿达姆斯公式(以四节点插值为例 假定己经算出,-’y,-2yn-’y的值,则y=f(x,y) (k=n-3,n-2,n-1,n)可计算给出。 y是x的函数,何以看作是的一元函数 因此,在区间,x)上可以用 外插值 的数 p(x)近似替代。 内插值 p)≈f) 鹏 X胖料
阿达姆斯公式可计算给出。 假定已经算出 , , , 的值,则 ( 3, 2, 1, ) ( , ) 3 2 1 k n n n n y y y y f f x y n n n n k k k = − − − − − − = y是x的函数,f可以看作是x的一元函数, 近似替代。 因此,在区间( ) 上 可以用其插值函数 ( ) , 1 p x x x f n n+ p(x) f(x) xn-3 xn-2 xn-1 xn 外插值 xn-2 xn-1 xn xn+1 p(x) f(x) 内插值 (以四节点插值为例) n−3 x n−2 x n−1 x n x n+1 x

阿达姆斯外推公式 由数值积分知识可知 如果以x?x2x’x为节点构造插值公式,则 p()d 6-7 2y Yn-3,Yn-2:Yn-1,Yn 于是,y≈y(x,)+p(x)dk 均为已知量 y+2盘5f化,)-59x火.) +37f(x2,y.-2)-9f(xyn3】 显式、线性多步方法
阿达姆斯外推公式 如果以x n−3 ,x n−2 ,x n−1 ,x n 为节点构造插值公式,则 由数值积分知识可知,( ) + = − − + − − − 1 55 59 1 37 2 9 3 24 ( ) x n x n n n n n f f f f h p x dx 于是, 37 ( , ) 9 ( , ) 55 ( , ) 59 ( , ) 24 ( ) ( ) 2 2 3 3 1 1 1 1 − − − − − − + + + − + − + n n n n n n n n n n x n x n n f x y f x y f x y f x y h y y y x p x dx 显式、线性多步方法 yn-3 , yn-2 ,yn-1 ,yn 均为已知量

阿达姆斯内插公式 如果以x-2x-’x,x为节点构造插值公式,则 pexs=a+11 方程式左右两边 均含有未知变量 于是,x)+pxwk yn+1 =火+24Dfx少)+19x,) -5f(xn-y.)+f(x-2yn2】 隐式、线性多步方法
阿达姆斯内插公式 如果以x n−2 ,x n−1 ,x n ,x n+1 为节点构造插值公式,则 ( ) + = + + − − + − 1 9 1 19 5 1 2 24 ( ) x n x n n n n n f f f f h p x dx 于是, 5 ( , ) ( , ) 9 ( , ) 19 ( , ) 24 ( ) ( ) 1 1 2 2 1 1 1 1 − − − − + + + + − + + + + n n n n n n n n n n x n x n n f x y f x y f x y f x y h y y y x p x dx 隐式、线性多步方法 方程式左右两边 均含有未知变量 yn+1