第十章 重积分 一元函数积分学 重积分 多元函数积分学{ 曲线积分 曲面积分
第十章 一元函数积分学 多元函数积分学 重积分 曲线积分 曲面积分 重 积 分

第一为 第十章 二重积分的桡念与性质 一、引例 二、二重积分的定义与可积性 三、二重积分的性质
三、二重积分的性质 第一节 一、引例 二、二重积分的定义与可积性 二重积分的概念与性质 第十章
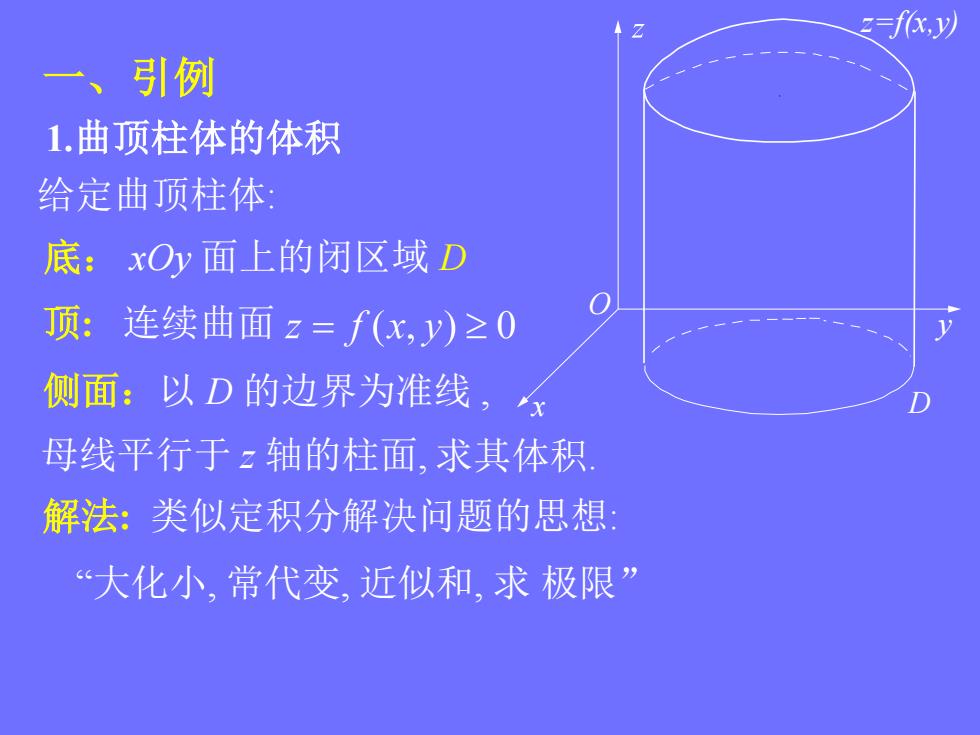
=f,y以 一、引例 1.曲顶柱体的体积 给定曲顶柱体: 底:xOy面上的闭区域D 顶:连续曲面z=f(x,y)≥0 1 侧面:以D的边界为准线, 母线平行于z轴的柱面,求其体积 解法:类似定积分解决问题的思想 “大化小,常代变,近似和,求极限
解法: 类似定积分解决问题的思想: 一、引例 1.曲顶柱体的体积 给定曲顶柱体: 底: xOy 面上的闭区域 D 顶: 连续曲面 侧面:以 D 的边界为准线 , 求其体积. “大化小, 常代变, 近似和, 求 极限” D z=f(x,y) x O 母线平行于 z 轴的柱面, y

E=f(x,y) 1)“大化小-分割” 用任意曲线网分D为n个区域 △o1,△o2,.,△om f(5,) 以它们为底把曲顶柱体分为n个 小曲顶柱体 2)常代变-取近似” 在每个△o中任取一点(5,7,),则 AV,≈f(5,7:)△o;(i=1,2,.,n 3)“近似和” V=2△y=J5,nAa
1)“大化小-分割” 用任意曲线网分D为 n 个区域 n , , , 1 2 以它们为底把曲顶柱体分为 n 个 2)“常代变-取近似” 在每个 3)“近似和” 1 ( , ) n i i i i f ( , ) ( 1,2, , ) V f i n i i i i 中任取一点 则 小曲顶柱体 D z=f (x,y) x O y
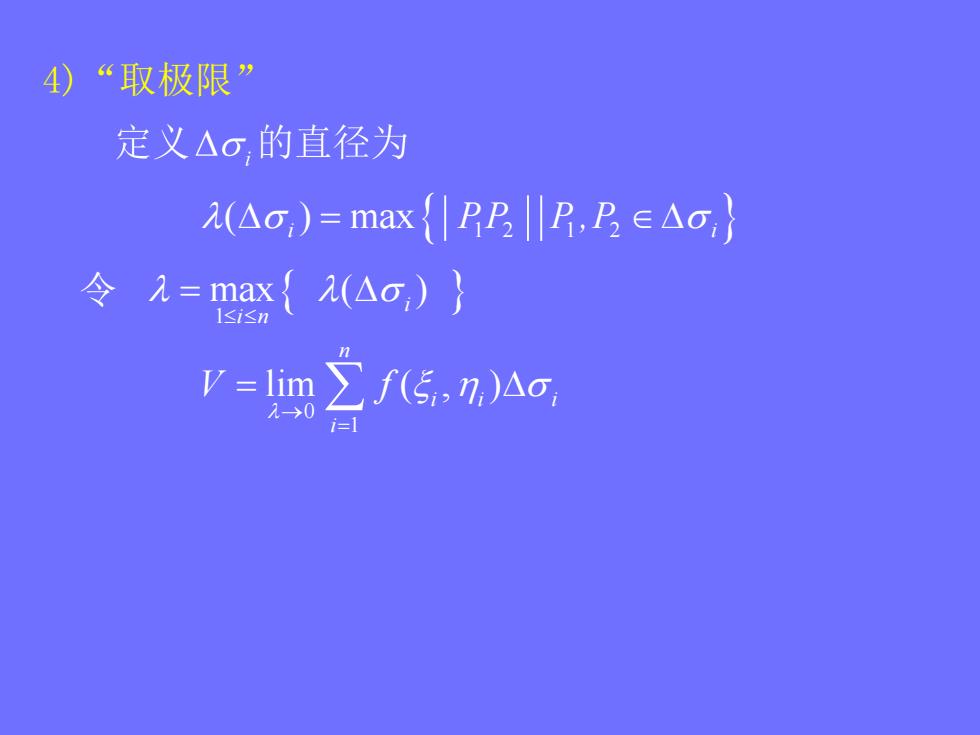
4)“取极限” 定义△o,的直径为 2(△o,)=maxP2B,∈Ao} 令元=max{2(△o,)} 1≤i≤n V =lim 2s0 ∑f5,n,)△o
4)“取极限” ( ) max i i PP P ,P 1 2 1 2 令 1 max ( ) i i n 0 1 lim ( , ) n i i i i V f