《高等数学》课程教学资源（课件讲稿）第十一章 曲线积分与曲面积分 11-1 对弧长的曲线积分

第十一章 曲线积与曲面积 积分学 定积分二 重积分三重积分曲线积分 曲面积分 积分域 区间 平面域 空间域 曲线弧 曲面域 对弧长的曲线积分 曲线积分 对坐标的曲线积分 对面积的曲面积分 曲面积分 对坐标的曲面积分

第十一章 积分学 定积分二重积分三重积分 积分域 区 间 平面域 空间域 曲线积分 曲线弧 曲面域 曲线积分 曲面积分 对弧长的曲线积分 对坐标的曲线积分 对面积的曲面积分 对坐标的曲面积分 曲面积分 曲线积分与曲面积分

第一节 第十一章 对狐长的曲线积分 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法

第一节 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法 对弧长的曲线积分 第十一章

一、对弧长的曲线积分的概念与性质 1.引例：曲线形构件的质量 假设曲线形细长构件L在xOy面所 占弧段为AB,其线密度为4(x,y)。 计算此构件的质量. x 匀质之质量M=4·S 变质之质量，采用 “大化小-分割，常代变-取近似，近似和，求极限

一、对弧长的曲线积分的概念与性质 假设曲线形细长构件L在xOy面所 占弧段为AB , 其线密度为 计算此构件的质量. 1.引例: 曲线形构件的质量 o x y A B L 匀质之质量 M s    . “大化小-分割, 常代变-取近似, 近似和, 求极限” 变质之质量，采用

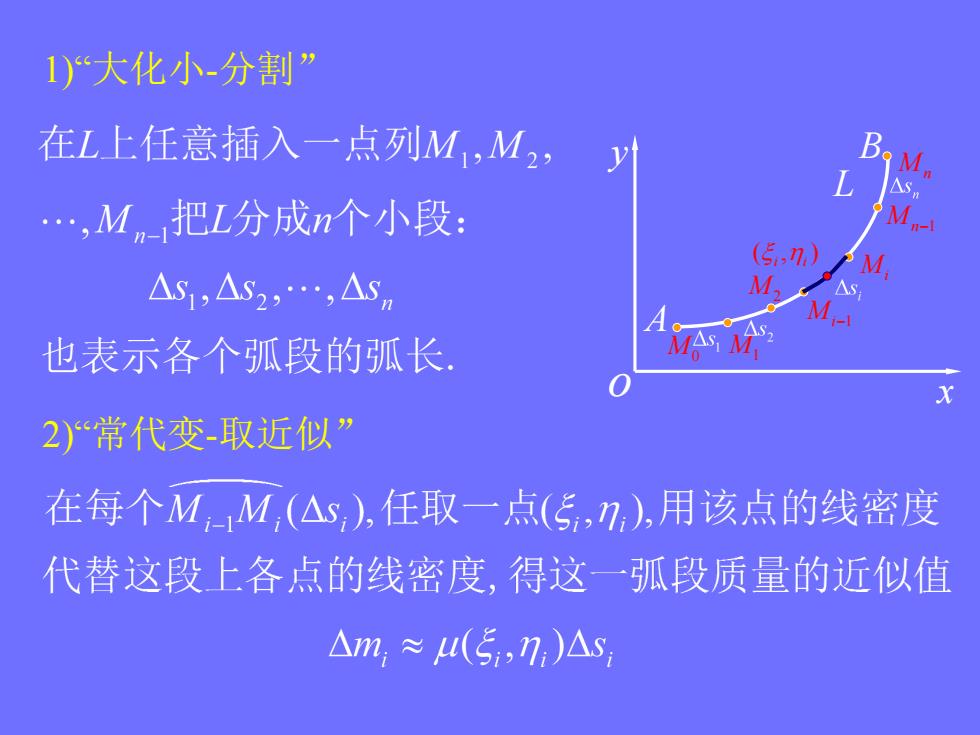
1)“大化小分割” 在L上任意插入一点列M,M2,y .,M,把L分成n个小段： M △S1,△S2,.,△S △s M 也表示各个弧段的弧长 X 2)常代变-取近似” 在每个MM,(△s),任取一点(5,7)，用该点的线密度 代替这段上各点的线密度，得这一弧段质量的近似值 △m,≈u(5,7,)△s

o x y A B M1M2 Mi1 MiM n1 L M0 M n 1)“大化小-分割” 2)“常代变-取近似” ( , ) i i  

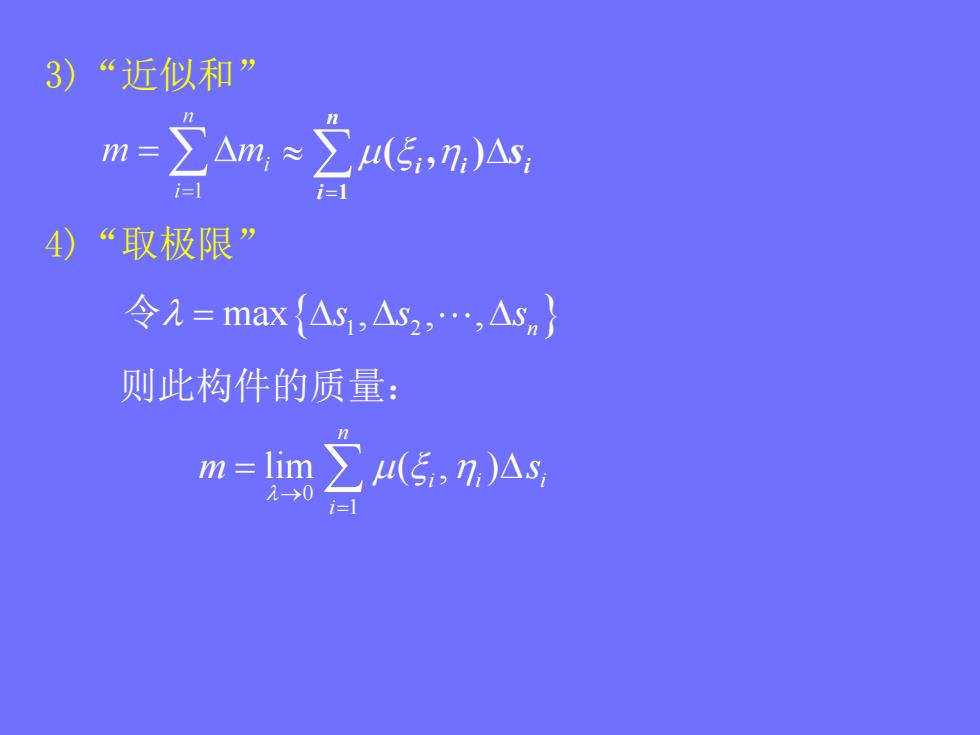
3)“近似和” m-n-2以5， 4)“取极限” 令=max{△s,△s,.,△sn} 则此构件的质量： m=∑4(5,7)△s 1→0 i=

3)“近似和”        1 ( , ) n i i i i s 4)“取极限” 令     max , , ,  s s s 1 2 n  0 1 lim ( , ) n i i i i m s          则此构件的质量：