《高等数学》课程教学资源（课件讲稿）第九章多元函数微分法及其应用 9-4 多元函数求导法则

第四方 第九章 多元复合品数的求导法则 元复合函数 y=f(u),u=p(x) 求导法则 dy dy du dx du dx 微分法则 dy=f"'(u)du=f'(u)o'(x)dx 本节内容： 一、多元复合函数求导的问题 二、多元复合函数的全微分

第四节 一元复合函数 求导法则 本节内容: 一、多元复合函数求导的问题 二、多元复合函数的全微分 微分法则 多元复合函数的求导法则 第九章 yu x

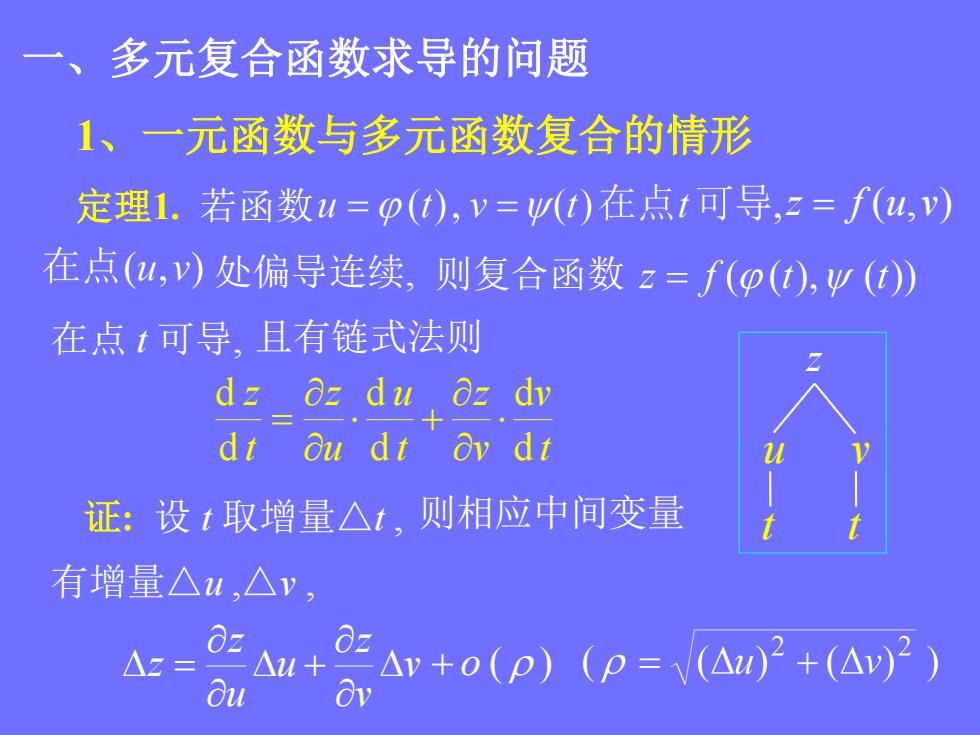
一、多元复合函数求导的问题 1、一元函数与多元函数复合的情形 定理1.若函数u=p(t),v=w(t)在点1可导，z=f(u,v) 在点(u,)处偏导连续，则复合函数z=f(p(t),y(t) 在点t可导，且有链式法则 dz Oz du oz dv dt Ou dt Oy dt 证：设t取增量△t,则相应中间变量 有增量△u,△v, △z= + Ou △y+o(p）(p=△w2+(A2) v

1、一元函数与多元函数复合的情形 定理1. 若函数 z  f (u,v) 处偏导连续, 在点 t 可导, t v v z t u u z t z d d d d d d         z 则复合函数 证: 设 t 取增量△t , v v z u u z z           o (  ) 则相应中间变量 且有链式法则 u v t t 有增量△u ,△v , 一、多元复合函数求导的问题

aEAu+A"+o(P）(p=V(△w2+(Ay2） △t ou△t Ov△t △ 令△t→0，则有△1→0，△v→0， △u du △vdv △t dt' △t dt 0(p) o(p) △t 0 (△1≤0时，根式前加“-号) dz Oz du Oz dv (全导数公式) dt Ou dt Oy dt

则有u  0, v  0, ( 全导数公式 ) t v v z t u u z t z             t o   (  ) z u v t t ( ( ) ( ) ) 2 2   u  v ( )  o   (△t＜0 时,根式前加“–”号) t v t v t u t u d d , d d       t v v z t u u z t z d d d d d d        

记忆：z=f(u,),u=p(t),v=Ψ(t), d=oz du oz dv dt au dt Ov dt 口诀：分段用乘，分叉用加， 单路全导，叉路偏导 推广：讨论中间变量多于两个的情形 设下面所涉及的函数都可微 例如，z=f(u,y,w), u=p(t),v=v(t),w=@(t) dz Oz du Oz dy Oz dw dt Ou dt Oy dt ow dt

推广: 讨论中间变量多于两个的情形. z  f (u,v,w) , 设下面所涉及的函数都可微 .  t z d d z u v w t u u z d d    t v v z d d     t w w z d d     u  (t), v  (t), w  (t) 例如, t t t 记忆: z f u v  ( , ) , u t v t     ( ), ( ), z u v t t  t z d d t u u z d d    t v v z d d     口诀 : 分段用乘, 分叉用加, 单路全导, 叉路偏导

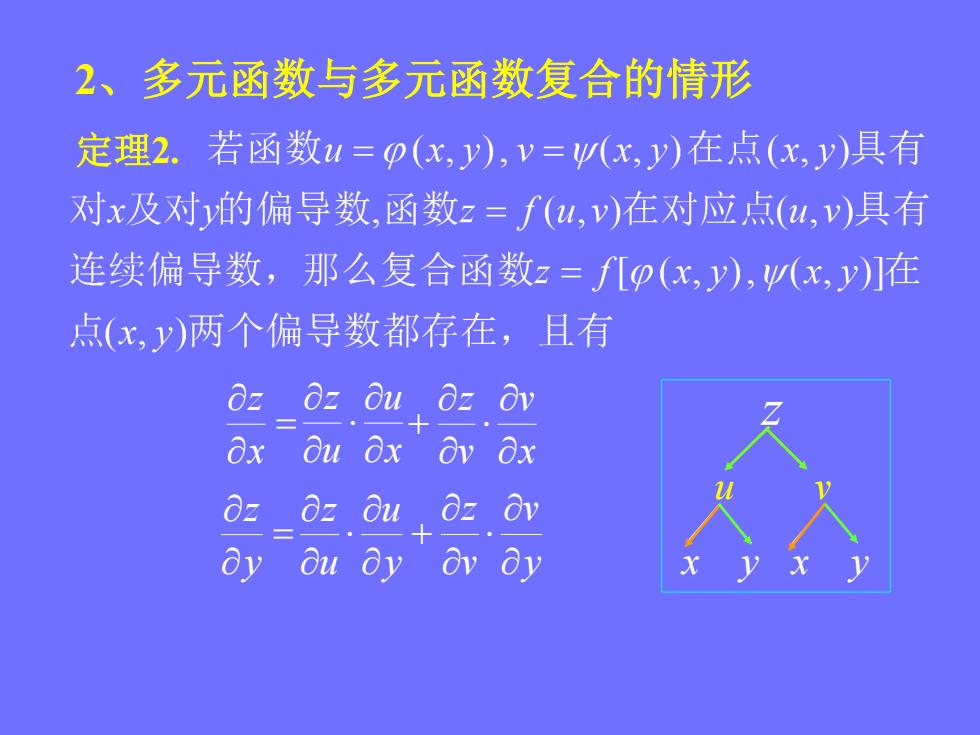
2、多元函数与多元函数复合的情形 定理2.若函数u=p(x,y),V=W(x,y)在点(x,y)具有 对x及对的偏导数，函数z=f(u,v)在对应点(u,v)具有 连续偏导数，那么复合函数z=fp(x,y),W(x,y)]在 点(x,y)两个偏导数都存在，且有 OzOz Ou 0z Ov Ox Ou Ox Bv 8x Oz oz ou Oz Ov ay Ou ay'av ay

2、多元函数与多元函数复合的情形 定理2.    x z    y z z u v x y x u u z      x v v z       y u u z      y v v z       x y