
第五节 第十一章 对望标的曲面积分 一、有向曲面及曲面元素的投影 二、对坐标的曲面积分的概念与性质 三、对坐标的曲面积分的计算法 四、两类曲面积分的联系
第五节 一、有向曲面及曲面元素的投影 二、 对坐标的曲面积分的概念与性质 三、对坐标的曲面积分的计算法 四、两类曲面积分的联系 对坐标的曲面积分 第十一章

一、有向曲面及曲面元素的投影 ·双侧曲面 曲面分内侧利 外侧 曲面分上侧和 曲面分左侧和 下侧 右侧
一、有向曲面及曲面元素的投影 • 双侧曲面 曲面分上侧和 下侧 曲面分内侧和 外侧 曲面分左侧和 右侧
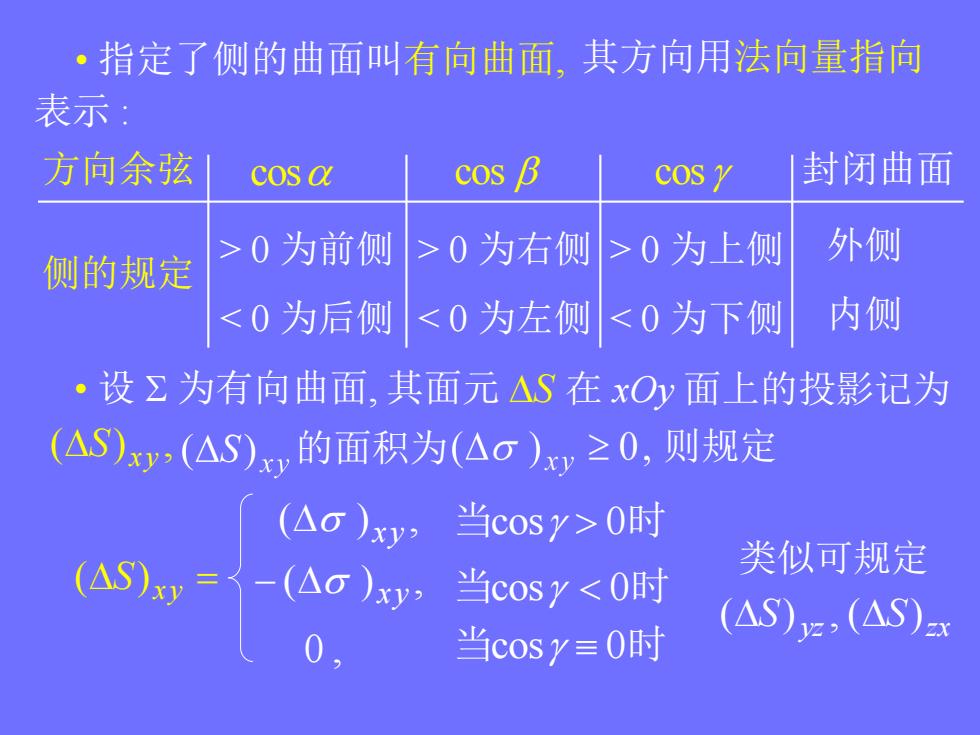
·指定了侧的曲面叫有向曲面,其方向用法向量指向 表示 方向余弦 cos a cos B cos y 封闭曲面 > >0为右侧>0为上侧 外侧 侧的规定 0为前侧 <0为后侧 <0为左侧<0为下侧 内侧 ·设Σ为有向曲面,其面元△S在xOy面上的投影记为 (△S)xy,(△S)x,的面积为(△o)xy≥0,则规定 (△o)xy, 当cosy>0时 w-62 类似可规定 当cosy<0时 (△S)z,(△S)a 当cosy≡0时
其方向用法向量指向 方向余弦 cos cos cos > 0 为前侧 < 0 为后侧 封闭曲面 > 0 为右侧 < 0 为左侧 > 0 为上侧 < 0 为下侧 外侧 内侧 • 设 为有向曲面, ( ) , xy S S (S) xy 侧的规定 • 指定了侧的曲面叫有向曲面, 表示 : 其面元 在 xOy 面上的投影记为 的面积为 则规定 ( ) , xy ( ) , xy 0 , 当cos 0时 当cos 0时 当cos 0时 类似可规定 S yz S zx ( ) , ( )

二、对坐标的曲面积分的概念与性质 1.引例设稳定流动的不可压缩流体的速度场为 V=(P(x,y,2),Qx,y,2),R(x,y,2) 求单位时间流过有向曲面Σ的流量Φ 分析:若是面积为S的平面, 法向量:n=(cosa,cosB,cosY) 流速为常向量: 则流量 Φ=S.cos0 =Sv.n
二、 对坐标的曲面积分的概念与性质 1. 引例 设稳定流动的不可压缩流体的速度场为 求单位时间流过有向曲面 的流量 . S 分析: 若 是面积为S 的平面, 则流量 法向量: 流速为常向量: n v

对一般的有向曲面Σ,对稳定流动的不可压缩流体的 速度场V=(P(x,y,2),Q(x,y,2),R(x,y,2》 用“大化小,常代变,近似和,取极限” 进行分析可得D=1im之可·,△S, >0 i=l 设,=(cos%,c0S,c0SY1),则 lim >[P(5m)cosa;+(5n5)cosB; 2-→0 +R(5,7,5i)cosY,]△S =mP5n5As),=+05,7,5As,)= 2>0 +R(5,1n,5i)(△S)xy]
Σ 对一般的有向曲面 , 用“大化小, 常代变, 近似和, 取极限” n i 1 0 lim 0 lim n i 1 P i i i i ( , , )cos R i i i i ( , , )cos 0 lim n i 1 Q i i i i ( , , )cos Si 对稳定流动的不可压缩流体的 速度场 进行分析可得 ni i v i ni Si v (cos , cos , cos ) ni i i i 设 , 则