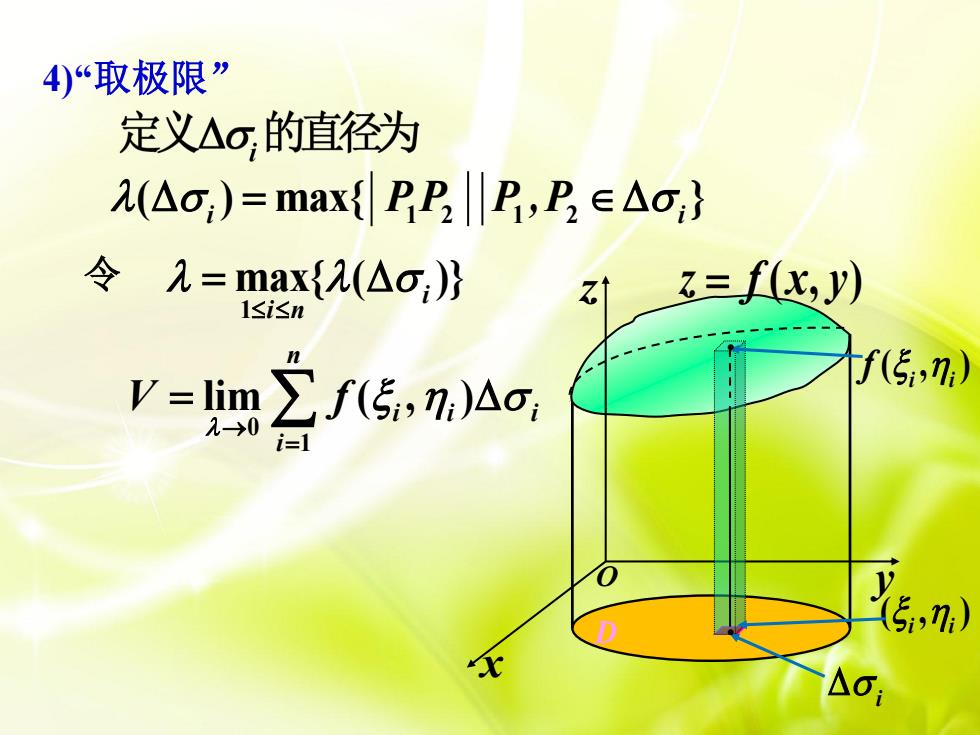
4)“取极限” 定义△o,的直径为 2(Ao,)=max{RE2lR,P∈△o} 令元=aAa,月 对3=f比y以 V=lim∑f5,7,)△o f(5,n,) 2-→0 i= 5,)
4)“取极限” 1 2 1 2 ( ) max{ } i i P P P ,P 令 1 max{ ( )} i i n 0 1 lim ( , ) n i i i i V f D z f x y ( , ) x z O y ( , ) i i ( , ) i i f i
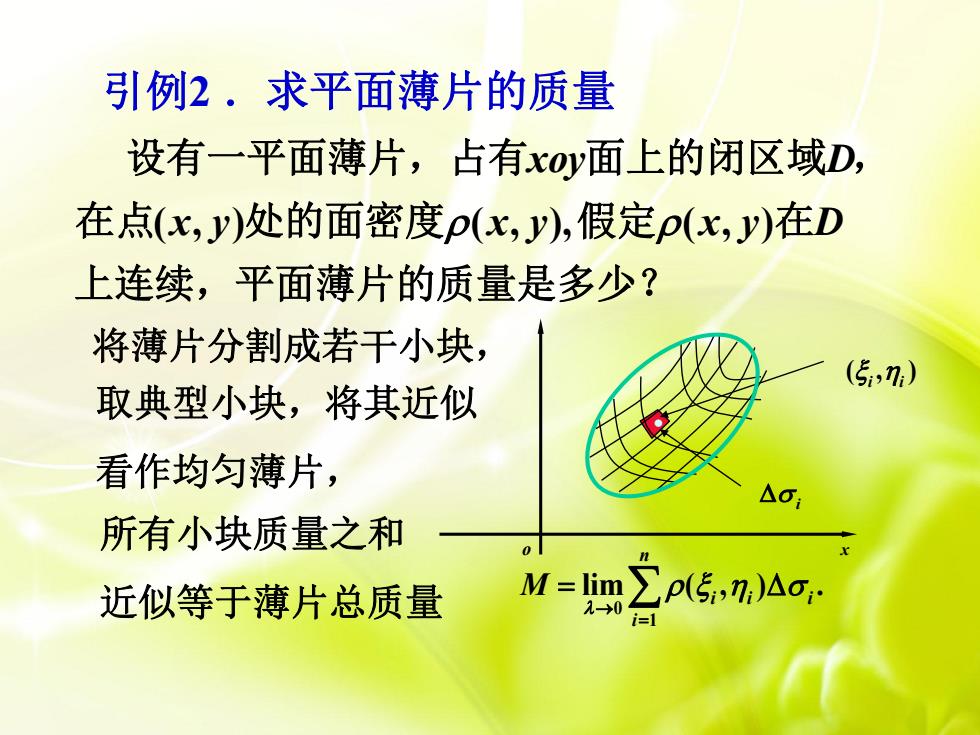
引例2.求平面薄片的质量 设有一平面薄片,占有xoy面上的闭区域D, 在点(x,y)处的面密度p(x,y),假定p(x,y)在D 上连续,平面薄片的质量是多少? 将薄片分割成若干小块, (5,7) 取典型小块,将其近似 看作均匀薄片, 所有小块质量之和 近似等于薄片总质量 M=∑p5nAa·
引例2 .求平面薄片的质量 i ( , ) i i 将薄片分割成若干小块, 取典型小块,将其近似 看作均匀薄片, 所有小块质量之和 近似等于薄片总质量 0 1 lim ( , ) . n i i i i M x y o ( , ) ( , ), ( , ) xoy D x y x y x y D 设有一平面薄片,占有 面上的闭区域 , 在点 处的面密度 假定 在 上连续,平面薄片的质量是多少?