
复变函数lim R~(z)=0 在 K,外部成立下面证明N-8-zo-令=与积分变量无关,0<9<1Z-ZoZ -Zo又因为f()≤M(由f(z)的连续性决定)f(S-z02dsR(z)≤2元JK-ZoZ - Zon=NN8MqM><h.2元ra2元1-qn=NU
11 下面证明 lim ( ) 0 . RN z 在 K1外部成立 N = → 0 0 0 z z r z z z q − = − − = 令 与积分变量 无关,0 q 1. 又因为 f ( ) M (由f (z)的连续性决定) s z z z z f R z K n N n N d ( ) 2π 1 ( ) 1 0 0 0 − − − = q r r M n n N = 2 2 1 . 1 q Mq N − =
复变函数所以L lim R(z) = 0.N-81 f()于是d2元iJKi-z80f(S)Z (z - Zo)-n=n=l8Z(z- Zo)-nC=n=1f(S)f(S)dsds则 f(z)-2元 iJKi- z2元 iJK2 - zU
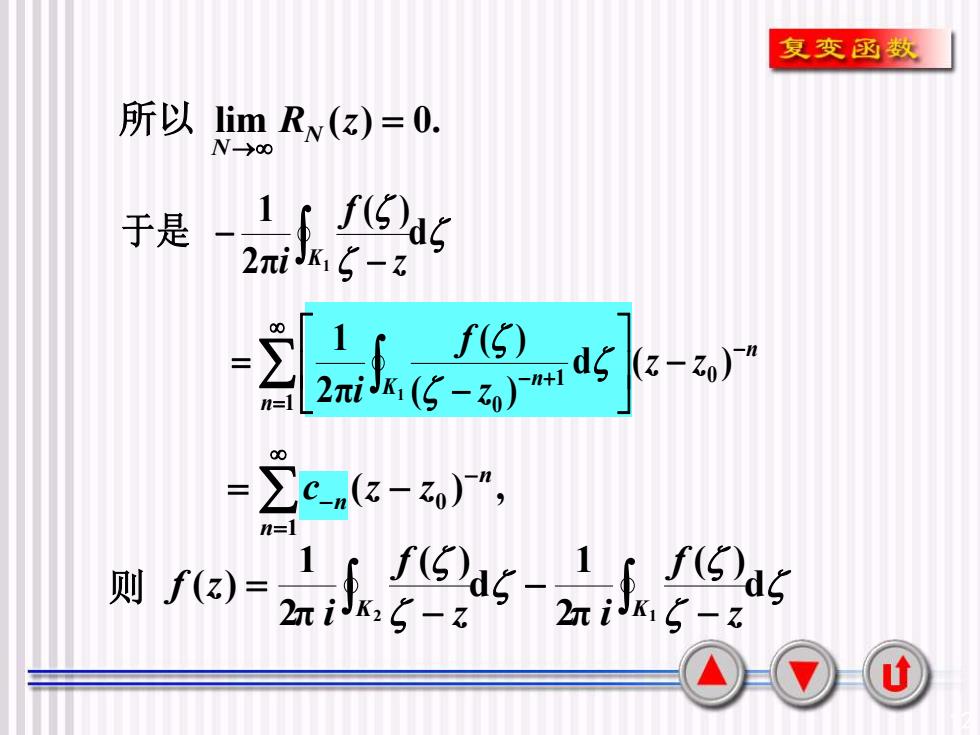
12 lim ( ) = 0. → R z N N 所以 ( ) , 0 1 n n n c z z − = = − − d ( ) 2π1 1 − − K z f i 于是 n n K n z z zf i − = − + − − = d ( ) ( ) ( ) 2π1 0 1 1 0 1 d ( ) 2π1 d ( ) 2π1 ( ) 2 1 − − − = K K z f z i f i 则 f z