
复变函数1所以 f(z)==z-1+1+z+z2+...+z"+..z(1 - z)即f(z)在 0<z<1内可以展开成级数,在圆环域0<z一1<1内,也可以展开成级数1f(z) =1-zz(1-z)z1-(1-z)[1 +(1 - z)+(1 - z)? + ...+(1 - z)" +1 - z= (1- z)-l +1+ (1-z) +(1- z)2 +(177山
6 所以 (1 ) 1 ( ) z z f z − = 1 , = z −1 + + z + z 2 ++z n + 即 f (z)在 0 z 1 内可以展开成级数. 在圆环域0 z −1 1内, 也可以展开成级数: (1 ) 1 ( ) z z f z − = (1 ) 1 (1 ) (1 ) (1 ) . = − z −1 + + − z + − z 2 + − z n−1 + + − + − ++ − + − = n z z z z 1 (1 ) (1 ) (1 ) 1 1 2 − − − = 1 (1 ) 1 1 1 z z

复变函数二、洛朗级数的概念定理设 f(z)在圆环域R<-zol<R,内处处解析,那末f(z)在D内可展开成洛朗级数8Zf(z) =Cn(z - Zo)",n=-80f()其中2mi (c-20)m dsCn为洛朗系数(n=0,±1,..)C为圆环域内绕的任一正向简单闭曲线U
7 二、洛朗级数的概念 定理 设 f (z)在圆环域R1 z − z0 R2内处处解析, ( ) ( ) , 0 n n n f z = c z − z =− + − = C n n z f i c d ( ) ( ) 2π 1 1 0 其 中 (n = 0, 1, ) C为圆环域内绕 0 的任一正向简单闭曲线. z 为洛朗系数. 那末 f (z)在 D内可展开成洛朗级数
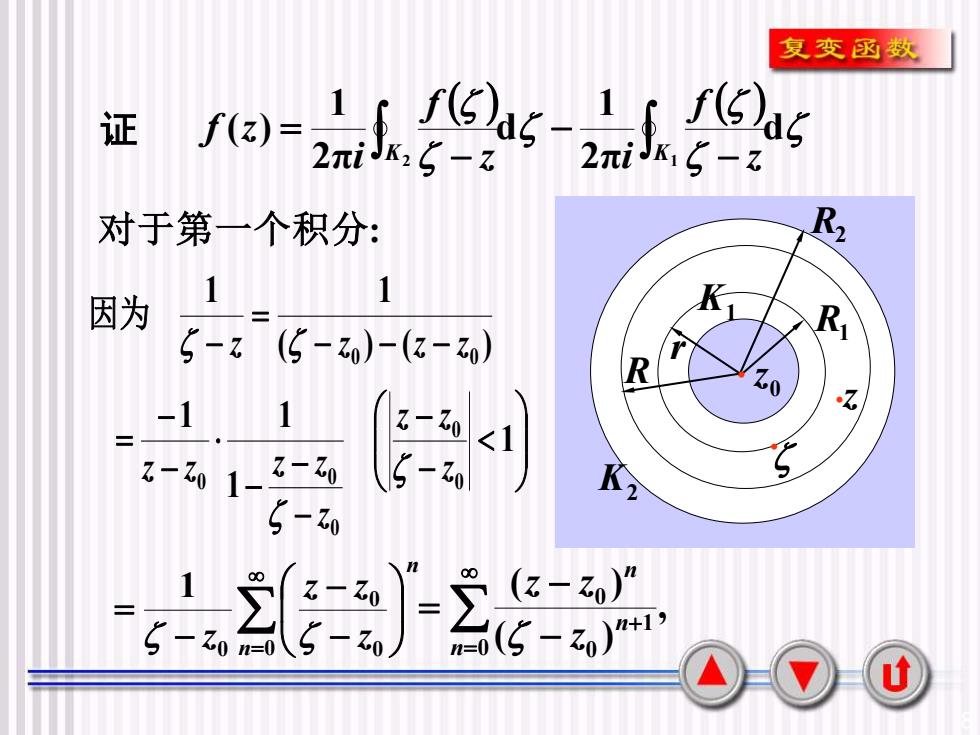
复变函数()d5 -f()ds1证f(z)-2元iJK2- z2元iJKl- zR2对于第一个积分1K因为R,-(-zo)-(z-zo)R1.07-1 1Z-Z0<1-S5- ZoZ-Zoz - zoK5-Zo118(z- Zo)nXz -Zo22(5 - z0)n+1)- zo n=20n=0U
8 ( ) ( ) d 2π 1 d 2π 1 ( ) 2 1 − − − = K K z f z i f i 证 f z ( ) ( ) 1 1 0 0 z − z − z − z = − 因为 对于第一个积分: = − − − = 0 0 0 0 1 n n z z z z − − − − − − − = 1 1 1 1 0 0 0 0 0 z z z z z z z z 0 R z r R2 .z K1 K2 R1 . . , ( ) ( ) 0 1 0 0 = + − − = n n n z z z

复变函数ihad所以180f(5)Z[2m f.(-(z- Zo)nds=n+1n=080Z(z- Zo)"=6?n=0f()ds对于第二个积分:2元iJK1-z1-1[≤-α<1因为S-Zo(z)-(z)Z-Zoz - zoZ-ZoU
9 n n n c (z z ) 0 0 = − = d ( ) 2π 1 2 K − z f i 所以 对于第二个积分: d ( ) 2π 1 1 K − z f i ( ) ( ) 1 1 0 0 z − z − z − z = − 因为 − − 1 0 0 z z z n n K n z z z f i d ( ) ( ) ( ) 2π 1 0 0 1 0 2 − − = = + 0 0 0 1 1 1 z z z z z − − − − − =

复变函数=-(5 -20)"-1800-2( -z0)-n+1(z- zo)",(z -Zo)"n=14 ()ds则2元iJK15- zN-f(S)Z[2f.dg[(z - Zo)-n + R(z)-n+1n=1A[26-21(6)]其中dR(z)=2元iJK(z-Zo)"n=NU
10 = − −− = − 1 0 1 0 ( ) ( ) n nn z z z ( ) , ( ) 1 0 1 1 0 n n n z z z − = − + − − = − d ( ) 2π1 1 − − K z f i 则 其中 R N ( z ) = d ( ) ( ) ( ) 2π1 1 01 0 − − = − K n N n n z z z f i d ( ) ( ) ( ) ( ) 2π1 0 11 1 0 1 z z R z zf i N n Nn K n − + − = − −= − +