
说明:若定理中f(u,)在点(u,v)偏导数连续 减弱为偏导数存在,则定理结论不一定成立 u'v 例如:=fu,)={w+,4+心≠0 u=t,v=t 0, 2+v2=0 Oz 易知:∂u . =f(0,0)=0,0z 0,0(0,0)=0 但复合函数乙=f(t,t)= t 2 dz 1 Oz du oz dy dt 2 Ou dt oy dt =01+01=0
说明: 若定理中 例如: 2 2 2 2 2 2 2 , 0 ( , ) 0, 0 u v u v z f u v u v u v u t v t , 易知: 但复合函数 ( , ) 2 t z f t t d 1 d 2 z t d d 0 1 0 1 0 d d z u z v u t v t 偏导数连续 减弱为偏导数存在,则定理结论不一定成立

2、多元函数与多元函数复合的情形 (z=f(u,v),u=p(x,y),y=y(x,y)的情形) 定理2如果函数u=p(x,y)及v=y(x,y)在点(x,y) 具有对x及对的偏导数,函数z=f(,)在对应点 (山,)具有连续偏导数,则复合函数z=fIp(x,y), (x,y)川在点(x,y)的两个偏导数都存在,且有 Oz Oz Ou Oz Ov Bx ou ax Oy ox Oz Oz ou 8y ou ay ov dy
2、多元函数与多元函数复合的情形 ( , ) ( , ) ( , ) ( , ) ( , ) [ ( , ), ( , )] ( , ) , . 2 u x y v x y x y x y z f u v u v z f x y x y x y z z u z v x u x v x z z u z v y u y v y 如果函数 及 在点 具有对 及对 的偏导数,函数 在对应点 具有连续偏导数,则复合函数 在点 的两个偏导数都存在,且有 定理 ( ( , ), ( , ), ( , ) ) z f u v u x y v x y 的情形
上述法则如图示 Ou 加加创
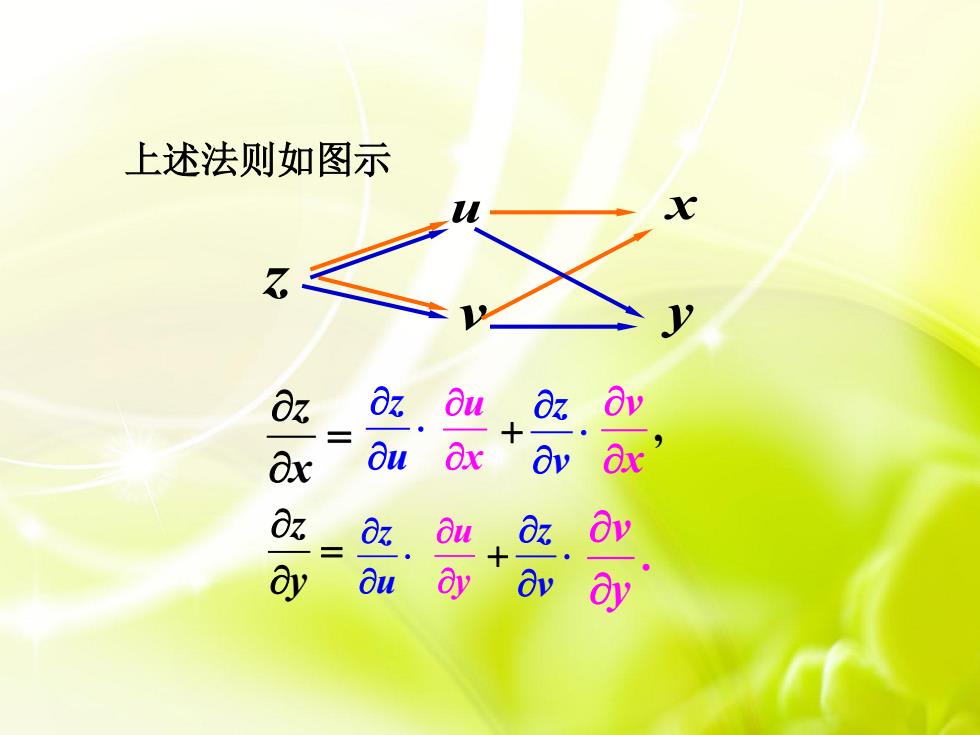
u v x z y 上述法则如图示 z x z u u x z v , v x z y z u u y z v . v y

类似地再推广,设u=p(x,y八v=(x,y)及w=w(x,) 在点(x,y)具有对x及对的偏导数,函数z=f(,y,w) 在对应点(,w)具有连续偏导数,则复合函数 z=fp(x,y),(x,y),w(x,y)川在点(x,y)的两个偏导数 都存在,且有 Oz Oz ou oz Ov Oz ow 一十 一+ Ox Ou ax Oy OxOw ax Oz Oz ou Ov Ow ay ou ay ov ay Ow Oy
z w v u y x , ( , ) ( , ) ( , ) ( , ) ( , , ) ( , , ) [ ( , ), ( , ), ( , )] ( , ) , u x y v x y w w x y x y x y z f u v w u v w z f x y x y w x y x y z z u z v z w x u x v x w x z z u y u y 类似地再推广 设 、 及 在点 具有对 及对 的偏导数,函数 在对应点 具有连续偏导数,则复合函数 在点 的两个偏导数 都存在,且有 . z v z w v y w y