
第五节曲面及其方程 ·一、曲面研宪的基本问题 ·二、旋转曲面 ·三、柱面与二次曲面 ·四、小结
第五节 曲面及其方程 • 一、曲面研究的基本问题 • 二、旋转曲面 • 三、柱面与二次曲面 • 四、小结

一、曲面研究的基本问题 例建立球心在M,(x,人半径为R的球面方程 解 设M(x,y,z)是球面上任意一点 根据题意有|MM,=R x-'+(0-)+(2-2=R 所求方程为(x-x}+(y-2+(a-z=R 特殊地:球心在原点时方程为x2+y2+z2=R 球面的一般方程为 Ax2+Ay2+Az2+Dx+Ey+Fz+G=0
解 根据题意有 | MM0 | R 2 2 2 0 0 0 x x y y z z R 2 2 0 2 0 2 所求方程为 x x0 y y z z R 特殊地:球心在原点时方程为 2 2 2 2 x y z R 2 2 2 0 Ax Ay Az Dx Ey Fz G 球面的一般方程为 0 0 0 0 例1 ( , , ) 建立球心在M x y z R 、半径为 的球面方程 一、曲面研究的基本问题 设M x y z ( , , )是球面上任意一点

例2求与原点O及M(2,3,4)的距离之比为1:2的点 的全体所组成的曲面方程。 解设M(K,y,z)是曲面上任意一点 根据题意有 M011 1MM2' x2+y2+32 V(x-2}+(y-3+(-421 所家方程为++(++)-
解 , 2 1 | | | | 0 MM MO 根据题意有 , 2 1 2 3 4 2 2 2 2 2 2 x y z x y z . 9 116 3 4 1 3 2 2 2 2 所求方程为 x y z 0 2 (2,3,4) 1 2 . 例 求与原点O M及 的距离之比为 :的点 的全体所组成的曲面方程 设M x y z ( , , )是曲面上任意一点

例3已知4A(1,2,3)B(2,-1,4),求线段AB的垂直平 分面的方程. 解设M(x,y,z)是所求平面上任一点, 根据题意有|MA=MB, V(x-1}+(y-2}+(a-3 =V(x-22+(0y+12+(a-4, 化简得所求方程2x-6y+2z-7=0
根据题意有 | MA || MB |, 2 2 2 x 1 y 2 z 3 2 1 4 , 2 2 2 x y z 化简得所求方程 2x 6 y 2z 7 0. 解 设M x y z ( , , ) , 是所求平面上任一点 3 (1,2,3) (2, 1,4) . 例 已知A B AB 、 ,求线段 的垂直平 分面的方程
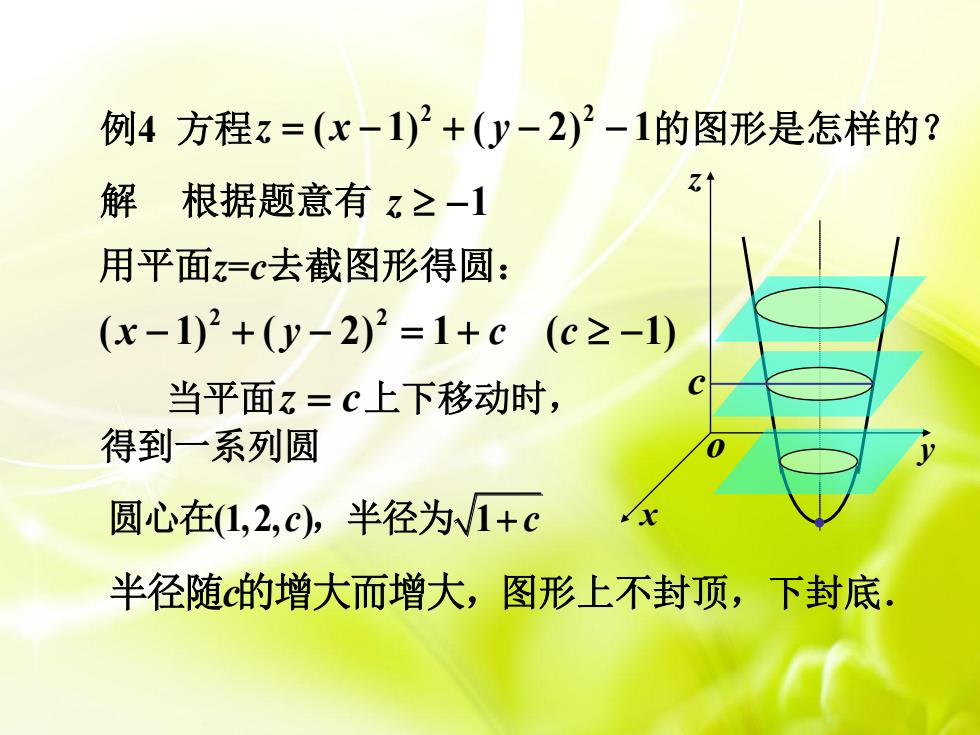
例4方程z=(x-1)2+(y-2)2-1的图形是怎样的? 解根据题意有z≥-1 71 用平面z=c去截图形得圆: (x-1)2+(y-2)2=1+c(c≥-1) 当平面z=C上下移动时, 得到一系列圆 圆心在(1,2,c,半径为V1+c 半径随c的增大而增大,图形上不封顶,下封底
z x o y 例4 方程 ( 1) ( 2) 1 的图形是怎样的? 2 2 z x y 根据题意有 z 1 ( 1) ( 2) 1 ( 1) 2 2 x y c c 当平面z c上下移动时, 得到一系列圆 图形上不封顶,下封底. 解 c 圆心在(1,2, ) 1 c c ,半径为 用平面z=c去截图形得圆: 半径随c的增大而增大