
例2计算Bx其中曲线AB是半径为的 圆在第一象限部分(方向按顺时针) 解引入辅助曲线L, L=0A+AB+BO 应用格林公式,P=0,Q=x有 0 ∬=∮=o,+∫6迹+∫o, 由于∫n4=0,∫nx=0, 。w=-可=子r
x y o L A B D L OA AB BO 应用格林公式,P=0,Q=x有 解 引入辅助曲线L, 2 ( ). AB xdy AB r 例 计算 ,其中曲线 是半径为 的 圆在第一象限部分 方向按顺时针 L D dxdy xdy , OA AB BO xdy xdy xdy 0, 0, OA BO xdy xdy 由于 1 2 . AB 4 D xdy dxdy r

练习计算J+3dx+0-dg 其中L为上半 圆周y=V4x-x2 从0(0,0)到A(4,0). 解:为了使用格林公式,添加辅助线段AO,它与L所围 区域为D,则 原式=∮o+3列dx+0-d +J(x+3y)dx+(-x)dy -4dxdy+dx 64 =8π+ 3
y o A x L 练习 计算 其中L 为上半 从 O (0, 0) 到 A (4, 0). 解: 为了使用格林公式, 添加辅助线段 AO, D 它与L 所围 原式 2 2 ( 3 ) d ( ) d L AO x y x y x 4 2 0 4 d d d D x y x x 2 2 ( 3 ) d ( ) d OA x y x y x y 圆周 区域为D , 则 64 8 3

刚3计算到, x2+y2 ,其中L是一条无重点分段 光滑且不经过原点的连续闭曲线,的方向为逆 时针方向. 解:记L所围成的闭区域为D, 则当x2+2≠0时,有=- ap ax (x2+y22 ay
解:记L所围成的闭区域为D, 2 2 3 L xdy ydx L x y L 例 计算 ,其中 是一条无重点分段 光滑且不经过原点的连续闭曲线, 的方向为逆 时针方向. 2 2 2 2 2 2 2 0 ( ) Q y x P x y x x y y 则当 时,有 2 2 2 2 , y x P Q x y x y 令

(1)当(0,0)ED时 由格林公式烈卓的出 0 (2)当(0,0)eD时 作位于D内的圆1:x2+y2=r2 记D由L和所围成, 应用格林公式,得
x y o L D 2 2 , 0 L xdy ydx x y 由格林公式知 L D1 r l y x o (1) (0, 0) 当 D时 2 2 2 作位于D l x y r 内的圆 : (2) (0, 0) 当 D时 应用格林公式,得 记D L l 1 由 和 所围成
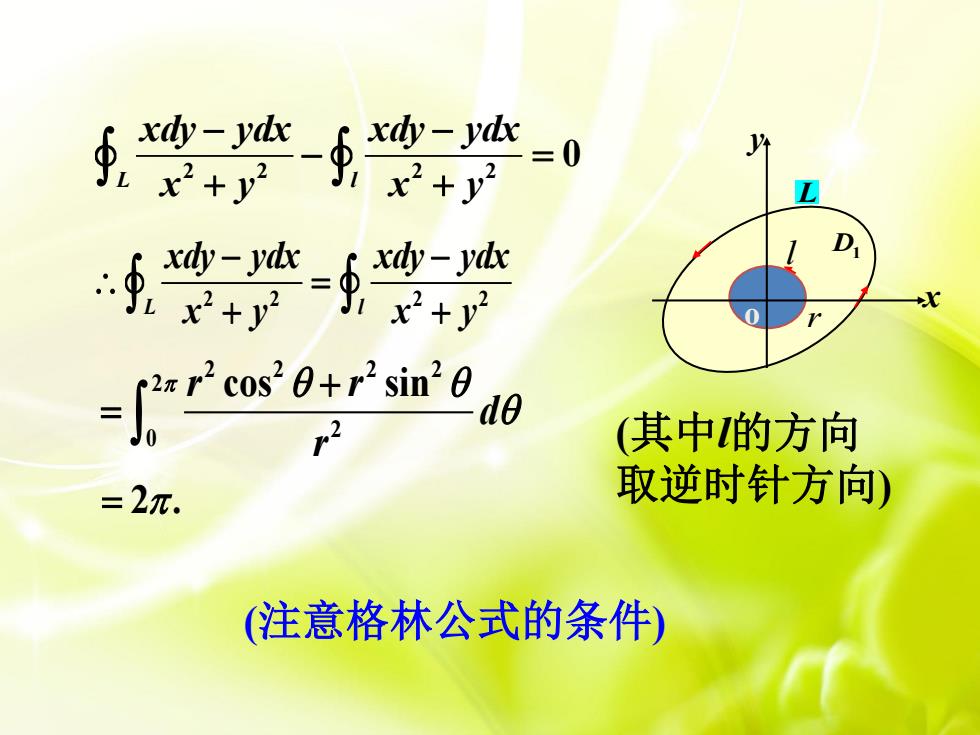
0 - rcs0+rsin 2d0 2 (其中的方向 =2m. 取逆时针方向) 注意格林公式的条件)
2 2 2 2 L l xdy ydx xdy ydx x y x y 2 2 2 2 0 L l xdy ydx xdy ydx x y x y 2 . (注意格林公式的条件) 2 2 2 2 2 2 0 r r cos sin d r L D1 r l y x o (其中l的方向 取逆时针方向)