
(2).简化二重积分 例4计算∬e“d,其中D是 由O(0,0),A(1,1),B(0,1)为顶 点的三角形闭区域: 解:令P=0,2=xe 则 2 OP=e ax ay
(2). 简化二重积分 x y o B A 1 1 D 2 4 (0,0), (1,1), (0,1) . y D e dxdy D O A B 例 计算 ,其中 是 由 为顶 点的三角形闭区域 2 0, y P Q xe 解:令 2 Q P y e x y 则

应用格林公式,有 ∬efa=∮xer 0A+AB+BO =∫a4ef=∫erk -e
2 2 y y D OA AB BO e dxdy xe dy 2 2 1 0 y x OA xe dy xe dx 1 1 (1 ). 2 e 应用格林公式,有

(3)计算平面面积 由格林公灯器-学a=手P肱+Q的 取P=-少e=x得,2∬=∮x-Jk 闭区域D的面积为:A=手,-心 另外,如果:取P=0,0=x,得A=∮ 取P=-以,2=0,得A=-∮J
, , 2 L D P y Q x dxdy xdy ydx 取 得 (3)计算平面面积 0, , L P Q x A xdy 取 得 , 0, L P y Q A ydx 取 得 1 2 L D A xdy ydx 闭区域 的面积为: ( ) L D Q P dxdy Pdx Qdy x y 由格林公式 另外,如果:
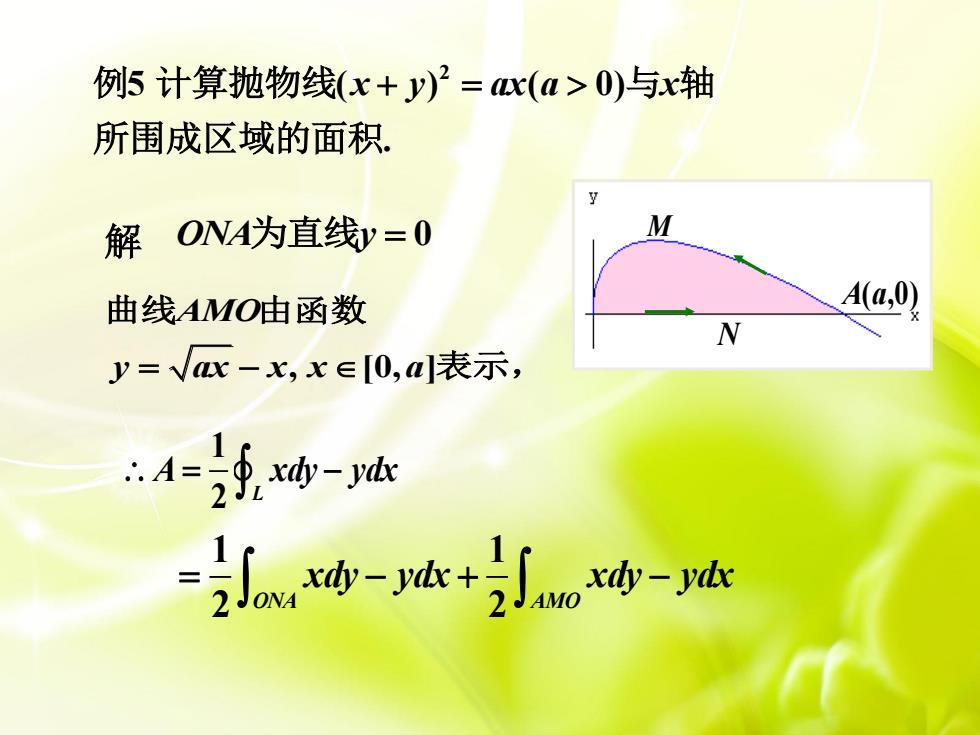
例5计算抛物线(x+y)2=x(a>0)与x轴 所围成区域的面积. 解ONA为直线y=0 M 曲线AMO由函数 A(a N y=Vx-x,x∈[0,a表示, ∴4- =迹-达+引n海-j肱
解 1 2 L A xdy ydx 1 1 2 2 ONA AMO xdy ydx xdy ydx A(a,0) N M 2 5 ( ) ( 0) . 例 计算抛物线 x y ax a x 与 轴 所围成区域的面积 ONA y 为直线 0 , [0, ] AMO y ax x x a 曲线 由函数 表示

=打o海-a Aa,0) N 2-(西-h =d
1 2 AMO xdy ydx 1 0 ( 1) ( ) 2 2 a a x dx ax x dx ax 2 0 1 . 4 6 a a xdx a A(a,0) N M