
有关内容复习: 拉格朗日(Lagrange)中值定理。 如果函数f(x)满足如下条件: (I)在闭区间[a,b]上连续; (2)在开区间(a,b)内可导; 则在(a,b)内至少有一点5,使得 )-I(b)-f(a) b-a
有关内容复习: 拉格朗日(Lagrange)中值定理。 如果函数 f x( ) 满足如下条件: (1) 在闭区间 上连续; (2) 在开区间 内可导; 则在 内至少有一点 ,使得 [ , ] a b ( , ) a b ( , ) a b ( ) ( ) ( ) f b f a f b a − = −
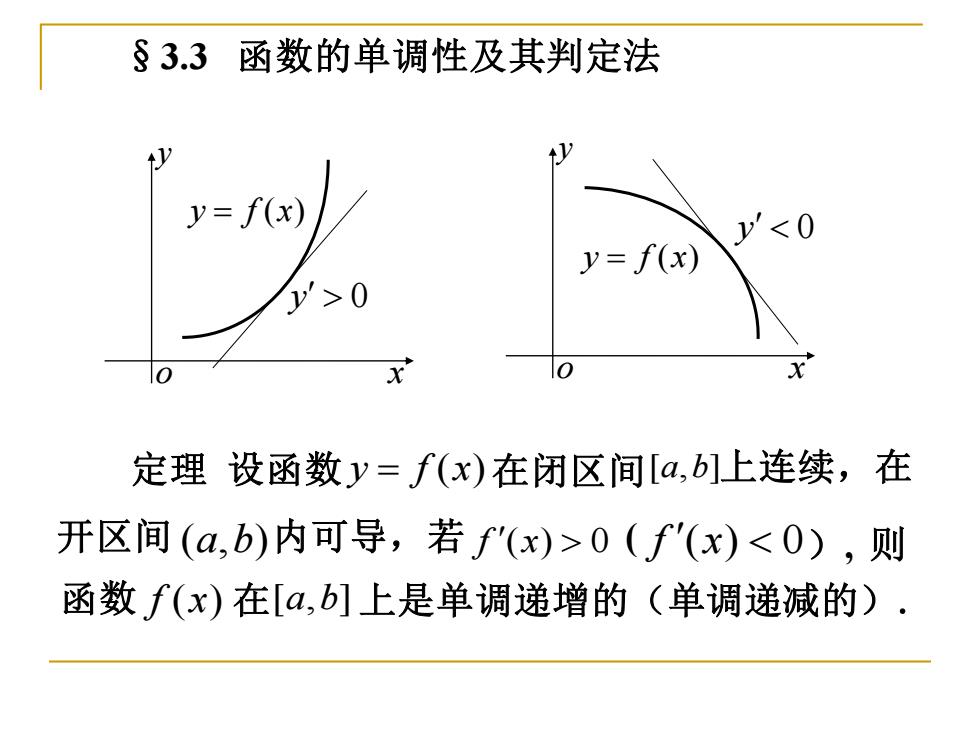
§3.3函数的单调性及其判定法 y=f(x) y<0 y=f(x) '>0 定理设函数y=f(x)在闭区间[a,b]上连续,在 开区间(a,b)内可导,若f'(x)>0(f'(x)<0),则 函数f(x)在[a,b]上是单调递增的(单调递减的)·
§3.3 函数的单调性及其判定法 y f x = ( ) [a,b] (a,b) f x ( ) 0 f x ( ) 0 f x( ) [a,b] 定理 设函数 在闭区间 在 上是单调递增的(单调递减的). 上连续,在 开区间 内可导,若 ( ), 则 函数 o x y y f x = ( )y 0 o x y y f x = ( ) y 0

注在定理中,若存在有限个点使得∫'(x)=0, 则函数f(x)在[a,b]上仍然是单调递增的(或单调 递减的);把定理中的闭区间换成其它任何区间, 定理的结论同样成立. 一般地,使得函数f(x)的导数f'(x)=0的点, 称为该函数的驻点。 例1判定函数y=x+cosx在[0,2π]上的单调性
注 在定理中,若存在有限个点使得 则函数 在 上仍然是单调递增的(或单调 递减的);把定理中的闭区间换成其它任何区间, 定理的结论同样成立. f x ( ) 0, = f x( ) [a,b] 一般地,使得函数 f x( ) 的导数 f x ( ) 0 = 称为该函数的驻点。 的点, 例1 判定函数 y x x = +cos 在 [0, 2 ] 上的单调性
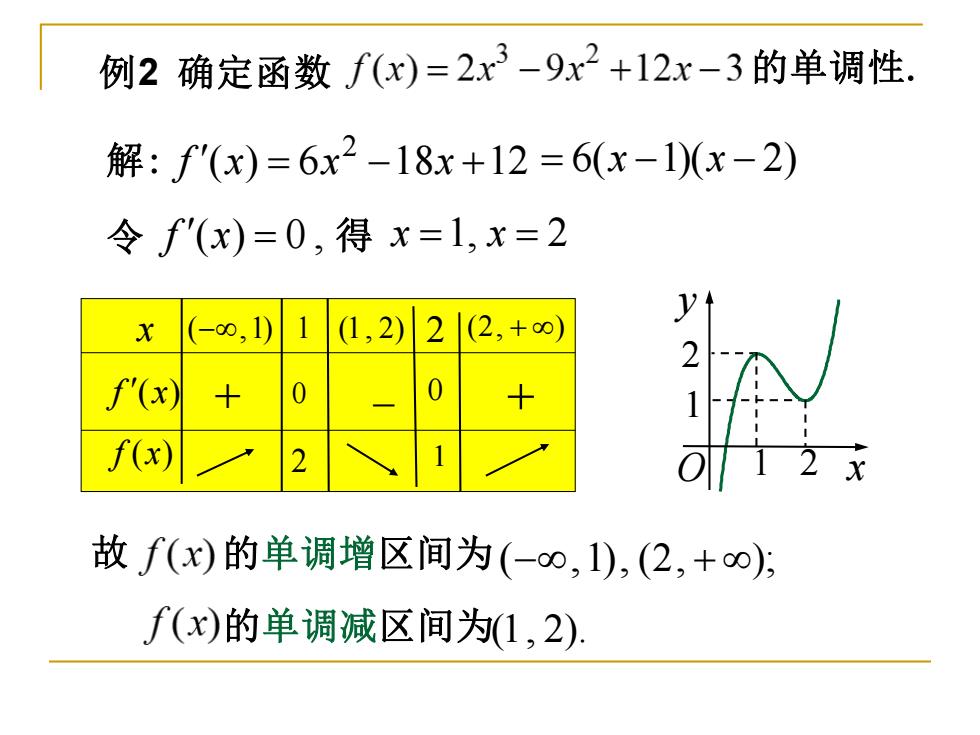
例2确定函数f(x)=2x3-9x2+12x-3的单调性. 解:f"(x)=6x2-18x+12=6(x-1)(x-2) 令f'(x)=0,得x=1,x=2 (-0,1)11,2)21(2,+) f(x (x) 故f(x)的单调增区间为(-o0,1),(2,+o): f(x)的单调减区间为(1,2)
例2 确定函数 的单调性. 解: ( ) 6 18 12 2 f x = x − x + = 6(x −1)(x − 2) 令 f (x) = 0 , 得 x =1, x = 2 故 的单调增区间为 (−,1), (2, + ); 的单调减区间为 (1, 2). 1 2 O x y 1 2 x f (x) f (x) (−,1) 2 0 0 1 (1, 2) (2, + ) + − + 2 1
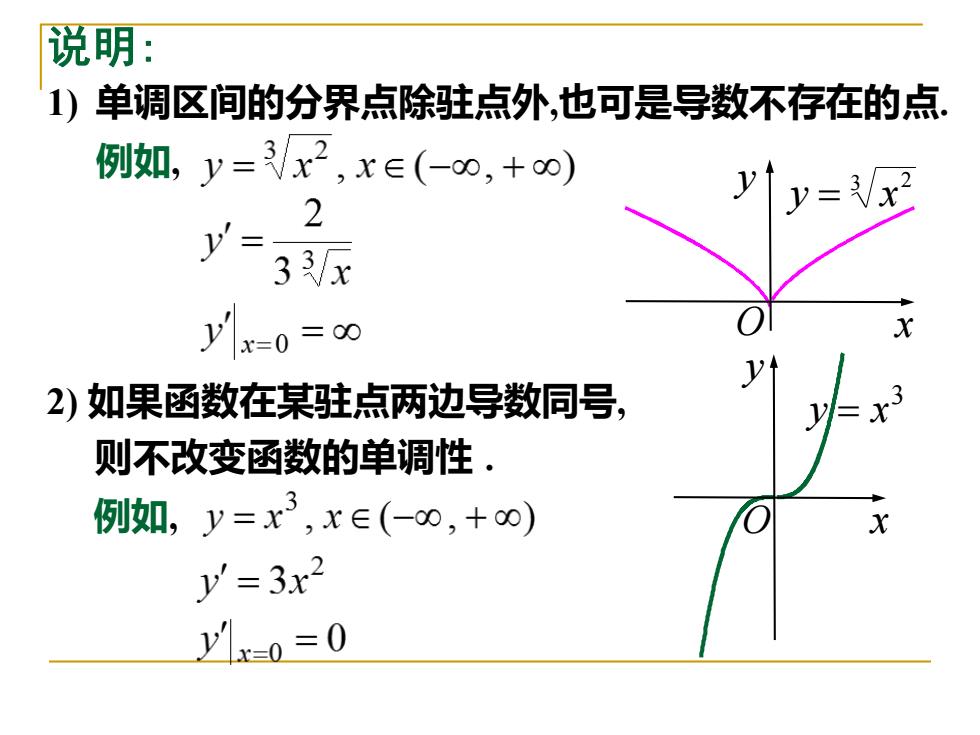
说明: 1)单调区间的分界点除驻点外,也可是导数不存在的点 例如,y=Vx2,xE(-0,+0) 2 y=Vx2 33 yx=0=0 2)如果函数在某驻点两边导数同号, 则不改变函数的单调性 例如,y=x3,xe(-0,+0) y'=3x2 y1k0=0
y O x 说明: 1) 单调区间的分界点除驻点外,也可是导数不存在的点. 例如, 3 2 y = x 2) 如果函数在某驻点两边导数同号, 则不改变函数的单调性 . 例如, y O x 3 y = x