
第五节 函数的微分 一、微分的概念 二、微分的几何意义 三、微分的计算 四、微分在近似计算中的应用
二、微分的几何意义 三、微分的计算 四、微分在近似计算中的应用 第五节 一、微分的概念 函数的微分
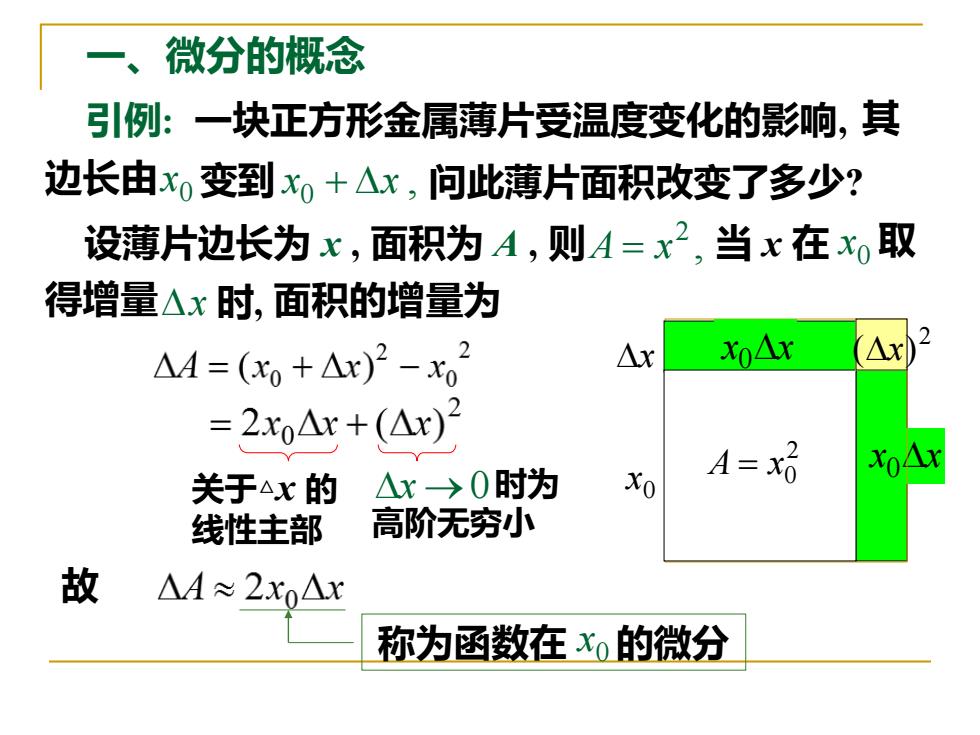
一、微分的概念 引例:一块正方形金属薄片受温度变化的影响,其 边长由xo变到xo+△x,问此薄片面积改变了多少? 设薄片边长为x,面积为A,则A=x2,当x在x取 得增量△x时,面积的增量为 △4=(0+△)2-02 △x xo△x △x2 =2xo△x+(△x) 关于△x的 △x→0时为 A=x好 线性主部 高阶无穷小 故 △A≈2xo△x 称为函数在x,的微分
x x 0 一、微分的概念 引例: 一块正方形金属薄片受温度变化的影响, 问此薄片面积改变了多少? 设薄片边长为 x , 面积为 A , 则 , 2 A = x 0 x x 面积的增量为 x x 0 2 0 A = x 2 (x) 关于△x 的 线性主部 高阶无穷小 x →0 时为 故 称为函数在 x0 的微分 当 x 在 0 x 取 得增量 x 时, 0 x 变到 , 0 边长由 x + x 其

定义:若函数y=f(x)在点xo的增量可表示为 △y=f(x+△x)-f(xo)=A△x+o(△x) (A为不依赖于△x的常数) 则称函数y=f(x)在点xo可微,而A△x称为f(x)在 点xo的微分,记作dy或df,即 dy=A△x 定理:函数y=f(x)在点x可微的充要条件是 y=f(x)在点xo处可导,且A=f'(xo),即 dy=f'(xo)△x
的微分, 定义: 若函数 在点 x0 的增量可表示为 ( A 为不依赖于△x 的常数) 则称函数 y = f (x) 而 Ax 称为 记作 即 dy = Ax 定理: 函数 在点 x0 可微的充要条件是 = Ax + o(x) 即 dy = f (x )x 0 在点 可微

定理:函数y=f(x)在点x,可微的充要条件是 y=f(x)在点xo处可导,且A=∫'(xo),即 dy=f'(xo)△x 证:“必要性” 已知y=f(x)在点xo可微,则 △y=f(x0+△x)-f(xo)=A△x+o(△x) lim Ay=lim (()=4 △x→0△X△x→0 △x 故y=f(x)在点x,可导,且∫'(xo)=A
定理 : 函数 证: “必要性” 已知 在点 可微 , 则 ( ) ( ) 0 0 y = f x + x − f x ) ( ) lim lim ( 0 0 x o x A x y x x = + → → = A 故 = Ax + o(x) 在点 可导, 且 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0

定理:函数y=f(x)在点x,可微的充要条件是 y=f(x)在点xo处可导,且A=f'(0),即 dy=f'(xo)△x “充分性”已知y=f(x)在点xo可导,则 lim Ay-f(xo) △x>0△x △y=f'(x0)+ y(lim a=0)) △x x0 故△y=f'(o)△x+aAx=f'(xo)Ax+o(△x) f'()≠0时 即dy=f'(x)△x 此项为y的 线性主部
定理 : 函数 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0 “充分性” 已知 lim ( ) 0 0 f x x y x = → = + ( ) 0 f x x y ( lim 0 ) 0 = → x y = f (x )x +x 故 0 ( ) ( ) 0 = f x x + o x 即 dy = f (x )x 0 在点 可导, 则