
上次课内容复习: 1、函数的单调性及其判定法; 2、曲线的凹凸性及其判定法; 3、函数图形的描绘。 本次课内容: 1、函数的极值及其求法 2、最大值与最小值问题
上次课内容复习: 1、函数的单调性及其判定法; 2、曲线的凹凸性及其判定法; 3、函数图形的描绘。 本次课内容: 2、最大值与最小值问题 1、函数的极值及其求法

§3.4函数的极值与最大值、最小值 一、函数的极值 定义:设函数f()在x,的某领域内有定义,若对 该邻域内异于的任意一点x都有 (1)f(x)<f(xo),则称x为f(x)的极大值点, 称f(xo)为函数的极大值; (2)f(x)>f(xo),则称xo为f(x)的极小值点, 称f(xo)为函数的极小值. 极大值点与极小值点统称为极值点
§3.4 函数的极值与最大值、最小值 (1) 则称 为 的极大值点 , 称 为函数的极大值 ; (2) 则称 为 的极小值点 , 称 为函数的极小值 . 极大值点与极小值点统称为极值点 . 一、函数的极值 定义: 设函数 f (x)在 的某领域内有定义,若对 该邻域内异于 的任意一点 ,都有
例如 函数f(x)=2x3-9x2+12x-3 x=1为极大值点,f1)=2是极大值 2 x=2为极小值点,f(2)=1是极小值 2 注意:1)函数的极值是函数的局部性质, 2)对常见函数,极值可能出现在导数为0或 不存在的点 x1,x4为极大值点 x2,x5为极小值点 x3不是极值点 a xt x2 x3 x4 xs b x
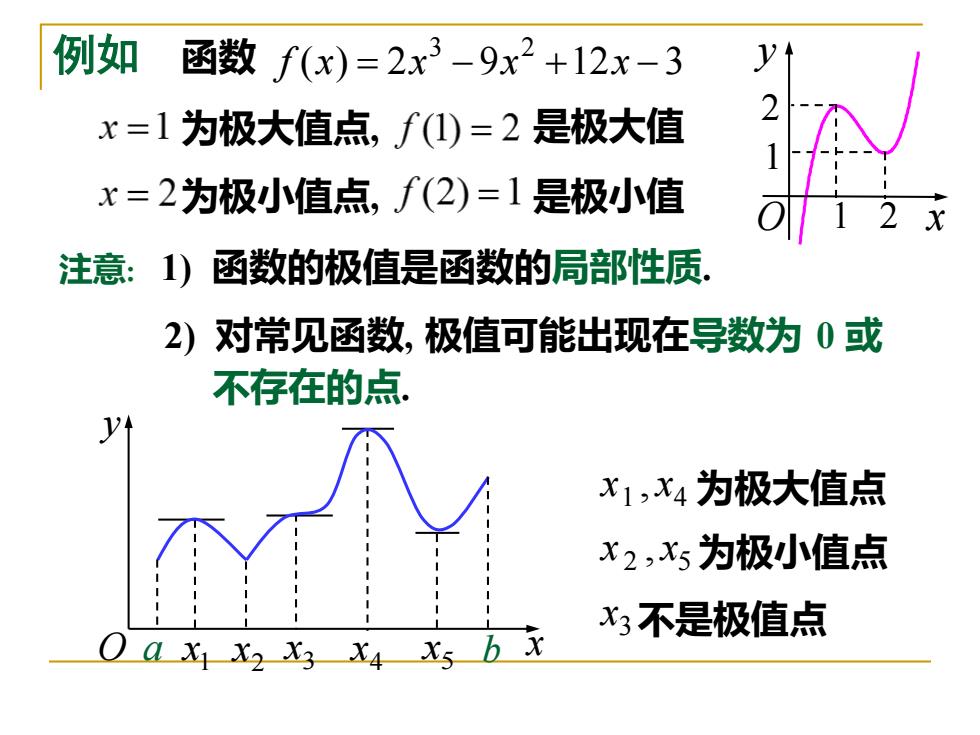
注意: 3 x 1 x 4 x 2 x 5 O a x b x y 1 4 x , x 为极大值点 2 5 x , x 为极小值点 3 x 不是极值点 2) 对常见函数, 极值可能出现在导数为 0 或 不存在的点. 1) 函数的极值是函数的局部性质. ( ) 2 9 12 3 3 2 例如 f x = x − x + x − 为极大值点, 是极大值 为极小值点, 是极小值 函数 1 2 O x y 1 2

定理1(必要条件) 设函数y=f(在点x 可导,且在处取得极值,则函数在点 x,处的导数 必为零,即 f'(x)=0 例讨论函数的极值点和极值 (1)f(x)=(x-1)2+2,(2)f(x)=x3 可导函数的极值点必为驻点,但是函数的驻点 不一定为极值点
y = f (x) 0 x 0 x 0 x f (x0 ) = 0 定理1 (必要条件) 设函数 在点 可导,且在 处取得极值,则函数在点 处的导数 必为零,即 。 可导函数的极值点必为驻点,但是函数的驻点 不一定为极值点. 例 讨论函数的极值点和极值 2 (1) f x x ( ) ( 1) 2 = − + (2) 3 , f x x ( ) =

定理2(第一充分条件)设函数f(x)在点x的 某邻域内连续,在点的去心邻域内可导,x为该去 心邻域内的任意一点,则 (I)若当x<x时,有f'(x)>0,当x>时,有f'(x)<0 则y=f(x)在点x,取得极大值; 2)若当x<x,时,有f'(x)<0,当x>x时,有f'(x)>0 则y=f(x)在点x,取得极小值; (③)若f'(x)在x的去心邻域内不变号,则f(x,)不是 极值
定理2 (第一充分条件) 设函数 在点 的 某邻域内连续,在点 的去心邻域内可导, 为该去 心邻域内的任意一点,则 (1) 若当 时,有 ,当 时,有 则 在点 取得极大值; (2) 若当 时,有 ,当 时,有 则 在点 取得极小值; (3) 若 在 的去心邻域内不变号,则 不是 极值. f x( ) 0 x 0 x x 0 x x f x ( ) 0 0 x x f x ( ) 0 y f x = ( ) 0 x 0 x x f x ( ) 0 0 x x f x ( ) 0 y f x = ( ) 0 x f x ( ) 0 x 0 f x( )