
上次课内容复习: 换元积分法 换元必换限 基本积分法 凑元不换限 分部积分法 边积边代限 §5.4定积分的几何应用 一、什么问题可以用定积分解决? 二、如何应用定积分解决问题?
上次课内容复习: 基本积分法 换元积分法 分部积分法 换元必换限 凑元不换限 边积边代限 §5.4 定积分的几何应用 一、什么问题可以用定积分解决 ? 二 、如何应用定积分解决问题 ?

一、什么问题可以用定积分解决? 1)所求量U是与区间[a,b]上的某分布fx)有关的 一个整体量; 2)U对区间[a,b]具有可加性,即可通过 “大化小,常代变,近似和,取极限” n 表示为U=lim∑f(5)△x 元→0 i=l 定积分定义 f(x)de=1imm∑f)Ay 2→01
表示为 一、什么问题可以用定积分解决? 1) 所求量 U 是与区间[a , b]上的某分布 f (x) 有关的 2) U 对区间 [a , b] 具有可加性 , 即可通过 “大化小, 常代变, 近似和, 取极限” 定积分定义 一个整体量 ;

二、如何应用定积分解决问题? 第一步利用“化整为零,以常代变”求出局部量 近腹值 微分表达式 dU=f(x)dx 第二步利用“积零为整,无限累加”求出整体量的 精确值 积分表达式 U-f(x)dx 这种分析方法成为元素法(或微元分析法) 元素的几何形状常取为:条,带,段,环,扇,片,壳等
二、如何应用定积分解决问题 ? 第一步 利用“化整为零 , 以常代变” 求出局部量 的 微分表达式 dU = f (x) dx 第二步 利用“ 积零为整 , 无限累加 ” 求出整体量的 积分表达式 U = f x x b a ( ) d 这种分析方法成为元素法 (或微元分析法) 元素的几何形状常取为: 条, 带, 段, 环, 扇, 片, 壳 等 近似值 精确值
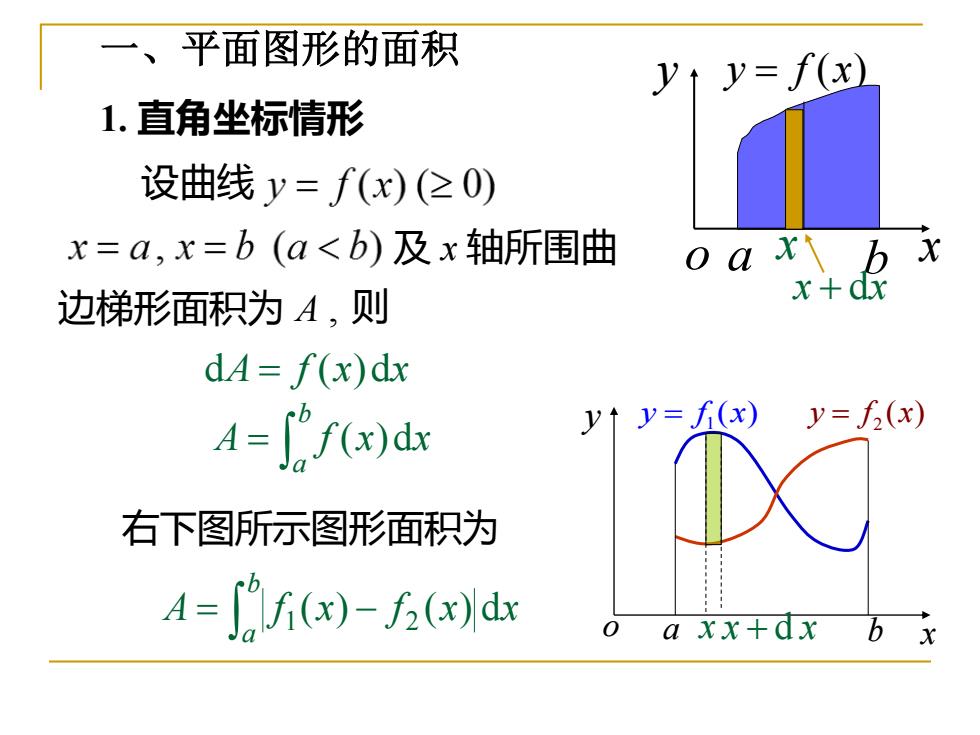
一、平面图形的面积 y↑y=f(x) 1.直角坐标情形 设曲线y=f(x)(20) x=a,x=b(a<b)及x轴所围曲 边梯形面积为A,则 x+dx dA=f(x)dx A-[f(x)dx y↑y=f(x)y=(x) 右下图所示图形面积为 4=[f(x)-f(x)dx o a xx+dx b x
一、平面图形的面积 1. 直角坐标情形 设曲线 及 x 轴所围曲 则 dA = f (x)dx A f x x b a ( )d = 边梯形面积为 A , o a b x y y = f (x) x x + dx y o a b x 2 y f x = ( ) 1 y f x = ( ) x x + d x 右下图所示图形面积为 A f x f x x b a ( ) ( ) d = 1 − 2
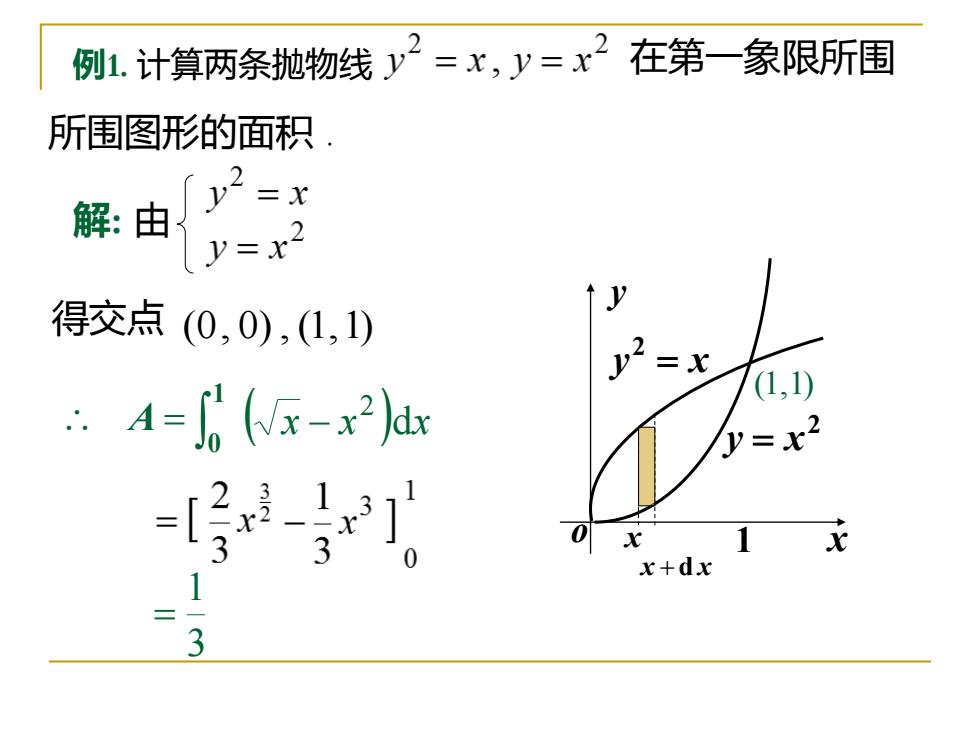
例1.计算两条抛物线y2=x,y=x2 在第一象限所围 所围图形的面积 解:由 y2=x J=x2 得交点0,0),1,1) =x .A=-x2)dx (1,1) P=x2 x+dx
例1. 计算两条抛物线 在第一象限所围 所围图形的面积 . x y = x 2 o y 2 y = x x 1 x + d x (1,1) 解: 由 得交点 (0, 0) , (1,1) d A ( x x )dx 2 = − 3 1 = = 1 0 A