
第二章 导数思想最早由法国 数学家Ferma在研究 导数与微分 极值问题中提出 微积分学的创始人: 英国数学家Newton 德国数学家Leibniz 导数 描述函数变化快慢 微分学 微分一 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数)
第二章 微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具 (从微观上研究函数) 导数与微分 导数思想最早由法国 数学家 Ferma 在研究 极值问题中提出. 英国数学家 Newton
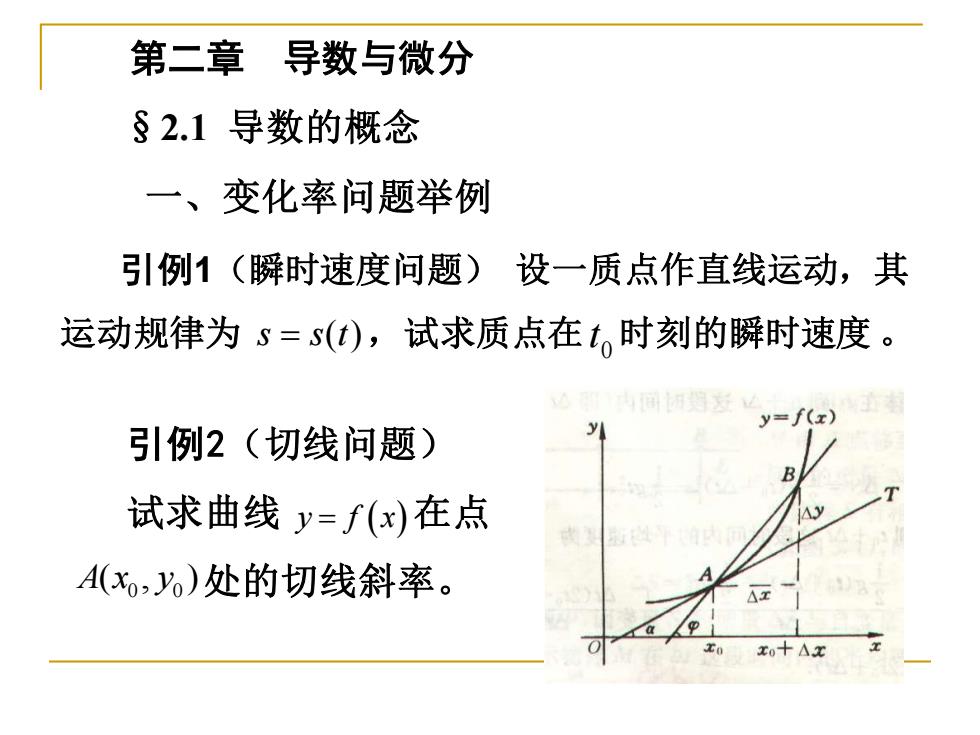
第二章 导数与微分 §2.1导数的概念 一、变化率问题举例 引例1(瞬时速度问题)设一质点作直线运动,其 运动规律为s=s(t),试求质点在t时刻的瞬时速度。 y=f(r) 引例2(切线问题) B 试求曲线y=f(x)在点 A(x,)处的切线斜率。 x0十△
第二章 导数与微分 §2.1 导数的概念 一、变化率问题举例 引例1(瞬时速度问题) 设一质点作直线运动,其 运动规律为 s s t = ( ) ,试求质点在 t 0 时刻的瞬时速度 。 引例2(切线问题) 试求曲线 在点 处的切线斜率。 y f x = ( ) 0 0 A x y ( , )

瞬时速度 v(6,)=lmA=lim (+△)-s() △t-→0△t △t→0 △t 切线斜率 k=lim f(x+△x)-f(x) △x→0 △x 两个问题的共性 所求量为函数增量与自变量增量之比的极限
( ) ( 0 0 ) ( ) 0 0 0 lim lim t t s s t t s t V t t t → → + − = = k ( 0 0 ) ( ) 0 lim x f x x f x → x + − = 两个问题的共性: 瞬时速度 切线斜率 所求量为函数增量与自变量增量之比的极限

二、导数的定义 1.函数在一点处的导数 定义设函数y=∫(x)在点x,的某邻域内有定义, 当自变量x在点,处有增量△x(。+△x点仍在该邻域 内),相应地函数的增量为△y=f(x+△x)-fx),如 果当Ax→0时,极限my-m+A)-() 存在, x→0△x△r-→0 △X 则称此极限为函数f(x)在点x,处的导数,记为f'(x,) 也可以记作'或倒 即 f(xo)=lim Ay=1imf+A)-f) (1) △x-→0△x △x→0 △x
二、导数的定义 1.函数在一点处的导数 定义 设函数 在点 的某邻域内有定义, 当自变量 在点 处有增量 ( 点仍在该邻域 内),相应地函数的增量为 ,如 果当 时,极限 存在, 则称此极限为函数 在点 处的导数,记为 也可以记作 , 或 . 即 (1) y f x = ( ) 0 x x 0 x x 0 x x + = + − y f x x f x ( 0 0 ) ( ) →x 0 ( 0 0 ) ( ) 0 0 lim lim x x y f x x f x → → x x + − = f x( ) 0 x 0 f x ( ) 0 x x y = 0 d d x x y x = ( ) 0 d d x x f x x = ( ) ( 0 0 ) ( ) 0 0 0 lim lim x x y f x x f x f x → → x x + − = =

在式(1)中,如果令x=x,+△x,则 △x=x-xAy=f(x)-f(x) 当△x→0时,x→x,从而式(1)变为 (x)=lim I(x)-f() (2) →x x-Xo 这也是今后常用的一种形式。 如果函数f(x)在点,处导数存在,则称f(x在点x 处可导,否则称∫(x)在点x处不可导
如果函数 在点 处导数存在,则称 在点 处可导,否则称 在点 处不可导. f x( ) 0 x f x( ) 0 x f x( ) 0 x 0 x x x = + 0 = − x x x = − y f x f x ( ) ( 0 ) 0 → → x x x 0时, 在式(1)中,如果令 ,则 当 ,从而式(1)变为 ( ) ( ) ( ) 0 0 0 0 lim x x f x f x f x → x x − = − (2) 这也是今后常用的一种形式