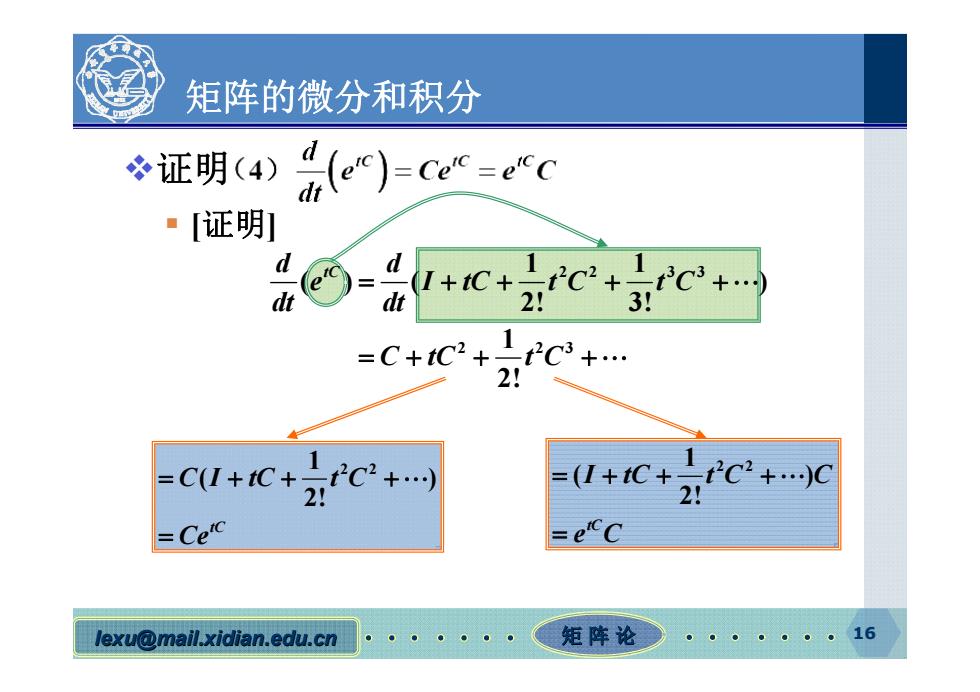
矩阵的微分和积分 证明4e)(e-ec 证明1 2! 31 1 =C+tC2+2C3+。 2! Cu+c+2fC+… =(+tC+C2+)0 2 lexu@mail.xidian.edu.cn 矩阵论 。。。。。。16
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 16 矩阵的微分和积分 证明 [证明] 22 33 2 23 1 1 () ( ) 2! 3! 1 2! d d tC e I tC t C t C dt dt C tC t C 1 2 2 ( ) 2! tC C I tC t C Ce 1 2 2 ( ) 2! tC I tC t C C e C

矩阵的微分和积分 矩阵积分定义 ·若矩阵A()=(a()mxn的每一个元素a)都是区 间[,上的可积函数,则称4()在区间[,上 可积 ·定义A(在,上的积分为 4oh-(a,ahn)nn lexu@mail.xidian.edu.cn 矩阵论 17
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 17 矩阵的微分和积分 矩阵积分定义 若矩阵A(t)=(ai,j(t))m×n的每一个元素ai,j(t)都是区 间[t0,t1]上的可积函数,则称A(t)在区间[t0,t1]上 可积 定义A(t)在[t0,t1]上的积分为 1 1 0 0 () () t t ij t t A t dt a t dt m n