
利用零化多项式求解矩阵函数 冬根据最小多项式求矩阵函数的一般方法 ·求出最小多项式 m(风=d.(2)=-2产2-)产…-严,2m=m ·形式上写出待定多项式 8)=2c=6,+c+6,2++cn ■求解关于待定系数的线性方程组 g(2)=f(2)(k=1,2,,m,;i=1,2,…,r) ·求出g(A),即可得f(A)=g(A) lexu@mail.xidian.edu.cn 矩阵论● 11
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 11 利用零化多项式求解矩阵函数 根据最小多项式求矩阵函数的一般方法 求出最小多项式 形式上写出待定多项式 求解关于待定系数的线性方程组 1 2 0 12 1 () () ( )( ) ( ) , r r mm m n ri i d mm 1 2 1 01 2 1 0 ( ) m i m i m i g c cc c c
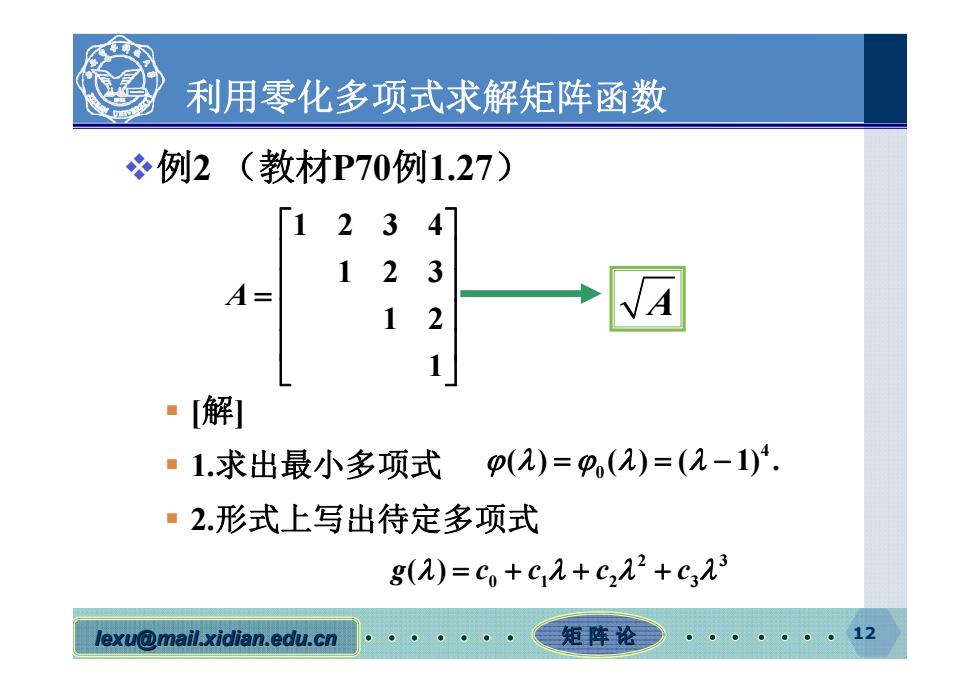
利用零化多项式求解矩阵函数 冬例2(教材P70例1.27) 1234 1 2 3 A- 1 2 ·解1 ·1.求出最小多项式p()=p(2)=(2-1)4. ·2形式上写出待定多项式 g(2)=c+c,2+c222+c323 lexu@mail.xidian.edu.cn 矩阵论 12
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 12 利用零化多项式求解矩阵函数 例2 (教材P70例1.27) [解] 1.求出最小多项式 2.形式上写出待定多项式 1234 123 1 2 1 A A 4 0 ( ) ( ) ( 1) . 2 3 01 2 3 g cc c c ( )

利用零化多项式求解矩阵函数 冬3求解系数线性方程组 1 80=f0=1=,+c+6+680=f0=2c+26,+3c g"=j"0=-}2+6eg0=f0 4 36c3 8 C3= 16 1 4.求出g(A),即可得A)g(A)8A=65I+151-5A+4) 「1111] 111 f(A)= 1 1 1 lexu@mail.xidian.edu.cn 矩阵论 13
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 利用零化多项式求解矩阵函数 3.求解系数线性方程组 4.求出g(A) ,即可得f(A)=g(A) 13 0123 g f cccc (1) (1) 1 123 1 (1) (1) 2 3 2 g f ccc 2 3 1 (1) (1) 2 6 4 g f cc 3 3 (1) (1) 6 8 gf c 32 10 1 5 15 5 , ,, 16 16 16 16 cc cc 1 2 3 ( ) (5 15 5 ) 16 gA I A A A 1111 111 ( ) 1 1 1 f A

矩阵的微分和积分 矩阵导数定义 ·若矩阵A()=(a)mXn的每一个元素a)是变量 t的可微函数,则称A()可微 ·其导数定义为 =A()= dA dt mxn ·类似地,可以定义矩阵高阶导数以及偏导数 lexu@mail.xidian.edu.cn 矩阵论 14
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 14 矩阵的微分和积分 矩阵导数定义 若矩阵A(t)=(ai,j(t))m×n的每一个元素ai,j(t)是变量 t的可微函数,则称A(t)可微 其导数定义为 类似地,可以定义矩阵高阶导数以及偏导数 ( ) ij m n dA da A t dt dt

矩阵的微分和积分 矩阵导数性质 ·A(),B()为可微矩阵,C为与t无关的矩阵,则 aD40±B01 d4±B dtdt (2)0B1=4B+ dt dt d 3) a0401 da _dt A+a dA dh 品eor(c刃=-csn(d ()-co() lexu@mail.xidian.edu.cn 矩阵论参 15
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 15 矩阵的微分和积分 矩阵导数性质 A(t), B(t) 为可微矩阵,C 为与t无关的矩阵,则