《线性代数》课程教学课件（PPT讲稿，B）第二章 矩阵与向量_2-1 消元法与矩阵的初等变换

最后，将方程组(2.5)的第二个方程的13倍加到第一个方程上， 将第二、三个方程分别乘以数-1/3,1/2，得到 X1=-1, x2=-2 (2.6) 七3=2. 加减消元法求解方程组的解，对方程组反复实施下列三种变换 (1)交换两个方程组的位置； (2)用一个非零的数乘以某一个方程； (3)把某个方程乘以一个常数后加到另一个方程上去。 我们把以上三种变换叫做线性方程组的初等变换。 线性方程组的初等变换不改变方程组的解

最后，将方程组(2.5)的第二个方程的1/3倍加到第一个方程上， 将第二、三个方程分别乘以数-1/3，-1/2，得到 , , .      1 2 3 = -1 = -2 = 2 x x x (2.6) 加减消元法求解方程组的解，对方程组反复实施下列三种变换 （1）交换两个方程组的位置； （2）用一个非零的数乘以某一个方程； （3）把某个方程乘以一个常数后加到另一个方程上去。 我们把以上三种变换叫做线性方程组的初等变换。 线性方程组的初等变换不改变方程组的解

矩阵概念 1.矩阵的定义 现在考虑一般元线性方程组 411X1+412X2+L+41mxn=b1, L21X1+022X2+L+42mXn=b2, (2.8) LLLLLLLLLLL amx am2x2+L amnxn bm 这个元线性方程组无法用克拉默法则来计算。 411412L ain L21L22 其未知量的系数构成的数表： Q2n L L am am2 L amn

二、矩阵概念 1.矩阵的定义 现在考虑一般n元线性方程组 , , .        11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b + + + = + + + = + + + = L L LLLLLLLLLLL L (2.8) 这个n元线性方程组无法用克拉默法则来计算。 其未知量的系数构成的数表： 11 12 1 21 22 2 1 2 n n m m mn a a a a a a a a a L L L L L

由m×个数a:(i=1,2,L,m;j=1,2,L,n) 排成的m行n列的数表，记作 411 42L L21 L22 L a2n (2.7) A= L L ami am2 L mn 称为m行n列矩阵(Matrix).简称m×n矩阵.简记为 A=(ag)n或Anm 矩阵一般用大写字母4，B,C,L来表示

简记为 ( ij)m n A a  = A mn 或 ( 1,2, , ; 1,2, , ) 由m n a i m j n  = = 个数 ij L L 排成的m n 行 列的数表，记作 称为m n 行 列矩阵(Matrix). 简称mn矩阵. 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a       =       L L L L L (2.7) 矩阵一般用大写字母A B C ,L 来表示

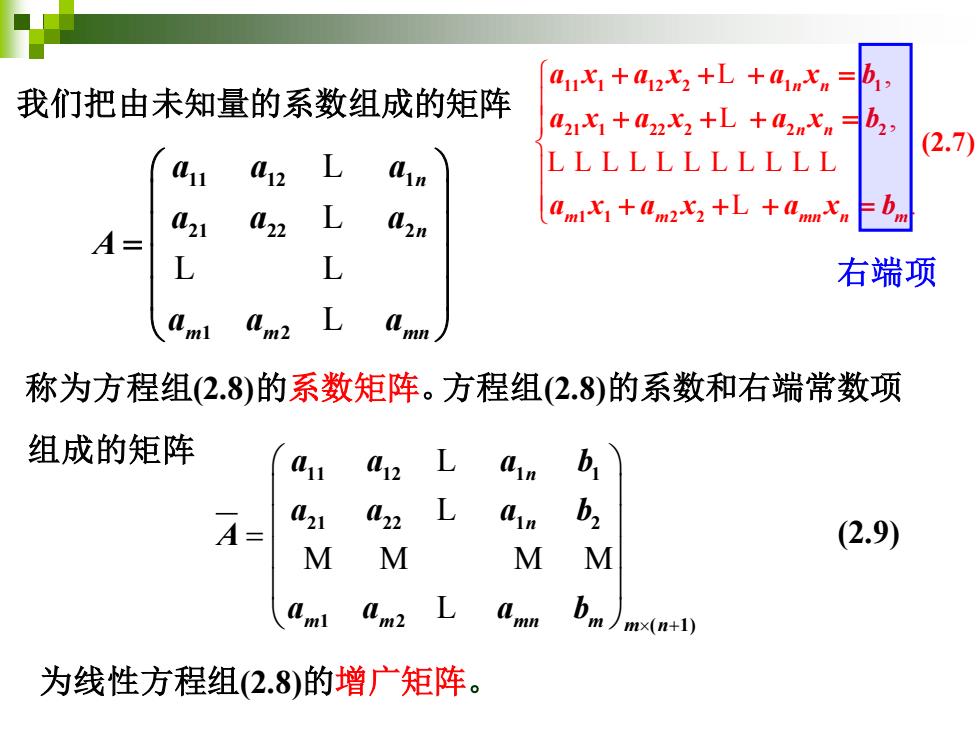
anx+azx2+L+aunx=b 我们把由未知量的系数组成的矩阵 azx+azx2+L +aznx =b2, (2.7 11 012 L LLLLLLLLLLL 1 L22 L amx+am2x2+LamFbm A= L 右端项 Am2 L 称为方程组(2.8)的系数矩阵。方程组(2.8)的系数和右端常数项 组成的矩阵 11 a12 L ain b L21 a L a A= (2.9) MM MM 4m bm)mx(n+1) 为线性方程组(2.8)的增广矩阵

我们把由未知量的系数组成的矩阵 为线性方程组(2.8)的增广矩阵。  +       =       11 12 1 1 21 22 1 2 1 2 ( 1) n n m m mn m m n a a a b a a a b A a a a b L L M M M M L (2.9) , , . 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b + + + = + + + = + + + =        L L LLLLLLLLLLL L (2.7) 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a       =       L L L L L 右端项 称为方程组(2.8)的系数矩阵。方程组(2.8)的系数和右端常数项 组成的矩阵

2.一些特殊的矩阵 零矩阵(Zero Matrix): 元素全为零的矩阵称为零矩阵， m×n零矩阵记作0mxn或O. 注意：不同阶数的零矩阵是不相等的. 例如： 0000 0000 ≠(000 0 00 0 0 000

2.一些特殊的矩阵 零矩阵(Zero Matrix): 注意： (0 0 0 0). 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0                不同阶数的零矩阵是不相等的. 例如： 元素全为零的矩阵称为零矩阵， mn 零矩阵记作 omn 或 o