
第十一章曲线积分与曲面积分 积分学 定积分二重积分三重积分曲线积分曲面积分 积分域 区间域 平面域 空间域 曲线域 曲面域 对弧长的曲线积分 曲线积分 对坐标的曲线积分 对面积的曲面积分 曲面积分 对坐标的曲面积分
山东农业大学 高等数学 主讲人:苏本堂 第十一章 曲线积分与曲面积分 积分学 定积分二重积分三重积分 积分域 区间域 平面域 空间域 曲线积分 曲线域 曲面域 曲线积分 曲面积分 对弧长的曲线积分 对坐标的曲线积分 对面积的曲面积分 对坐标的曲面积分 曲面积分

第一节对弧长的曲线积分 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法
山东农业大学 高等数学 主讲人:苏本堂 第一节 对弧长的曲线积分 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法
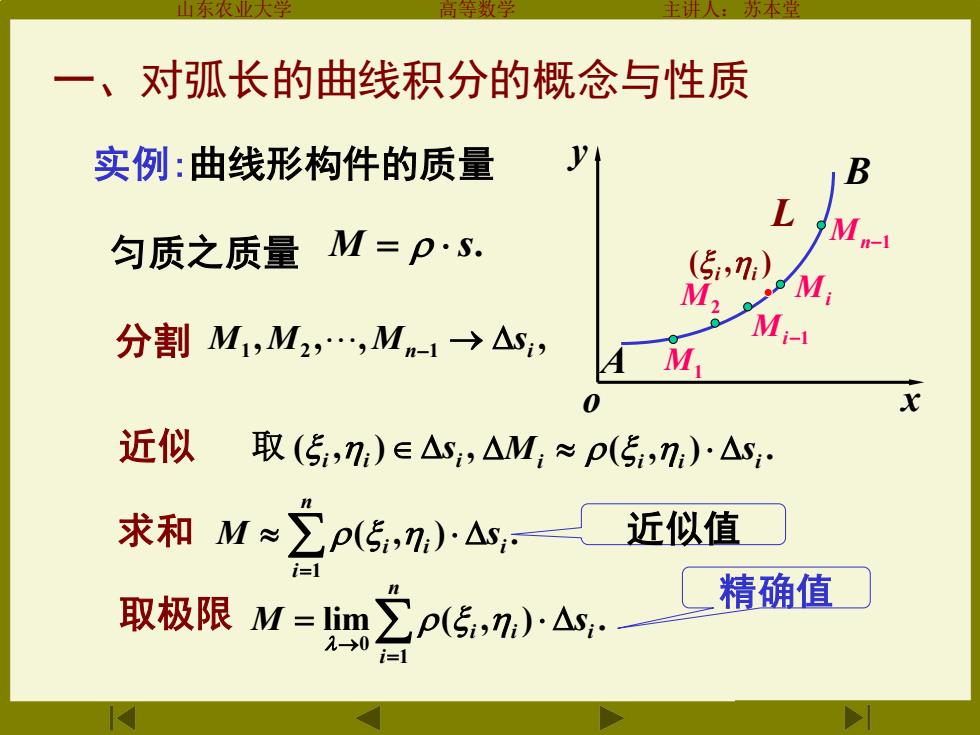
一、对弧长的曲线积分的概念与性质 实例:曲线形构件的质量 B L 匀质之质量M=p·S. M ,n) M2 M 分割M1,M2,.,Mn-1→△S, Mi A M 0 x 近似 取(5,n)∈△s,△M;≈p(5,n:)·△s 求和M≈∑p(5,n)Ay, 近似值 精确值 取极限M=im∑p(传,n,)△,. 2→0 i=1
山东农业大学 高等数学 主讲人:苏本堂 一、对弧长的曲线积分的概念与性质 实例:曲线形构件的质量 匀质之质量 M = s. o x y A B M1 M2 Mi−1 Mi Mn−1 L ( , ) i i 分割 , , , , 1 2 n 1 i M M M → s − ( , ) , i i i 取 s ( , ) . i i i i M s 求和 ( , ) . 1 = n i i i i M s 近似值 取极限 lim ( , ) . 1 0= → = n i i i i M s 精确值 近似

1.定义设L为xOy面内的一条光滑曲线弧,函数fx,y)在L 上有界.将L任意分成n个小弧段:△s1,△s2,··,△sn(△s,也表示 第个小弧段的长度);在每个小弧段△s上任取一点(5,7),作和 ∑f5,n)AS, i=l 如果当=max{△S1,△s2,··,△sm}→0时,这和的极限总存在,则 称此极限为函数x,y)在曲线弧L上对弧长的曲线积分,记作 Jfx还,即 fk=2EwA, 其中x,y)叫做被积函数,L叫做积分弧段
山东农业大学 高等数学 主讲人:苏本堂 1. 定义 设L为xOy面内的一条光滑曲线弧 函数f(x y)在L 上有界将L任意分成n个小弧段s1 s2 sn (si也表示 第i个小弧段的长度)在每个小弧段si上任取一点(i i ) 作和 i i i n i f s = ( , ) 1 i i i n i L f x y ds = f s → = ( , ) lim ( , ) 1 0 如果当=max{s1 s2 sn }→0时 这和的极限总存在 则 称此极限为函数f(x y)在曲线弧L上对弧长的曲线积分 记作 f x y ds L ( , ) 即 其中f(x y)叫做被积函数 L叫做积分弧段

山东 方本 对弧长的曲线积分 f(x.y)ds=m2f5n△. 注 1>0=1 •对弧长的曲线积分也称为第一类曲线积分 ·当函数孔x,y)在光滑曲线弧L上连续时,函数x,y)在曲线 弧L上对弧长的曲线积分是存在的.以后我们总假定孔x,y) 在L上是连续的. 如果L是闭曲线,则记为ff(x,y)ds. ·类似地定义函数孔x,y,z)在空间曲线弧「上对弧长的曲线 积分: f,y2ds=lm∑f5,n,5)△. 20i1
山东农业大学 高等数学 主讲人:苏本堂 i i i n i L f x y ds = f s → = ( , ) lim ( , ) 1 0 对弧长的曲线积分 注 •当函数f(x y)在光滑曲线弧L上连续时 函数f(x y)在曲线 弧L上对弧长的曲线积分是存在的 以后我们总假定f(x y) 在L上是连续的 •对弧长的曲线积分也称为第一类曲线积分 i i i i n i f x y z ds = f s → = ( , , ) lim ( , , ) 1 0 •类似地定义函数f(x y z)在空间曲线弧上对弧长的曲线 积分 •如果 L 是闭曲线 , 则记为 ( , )d . L f x y s