
主讲 苏本堂 第九章习题课 主要内容 典型例题
山东农业大学 高等数学 主讲人:苏本堂 第九章 习题课 主要内容 典型例题
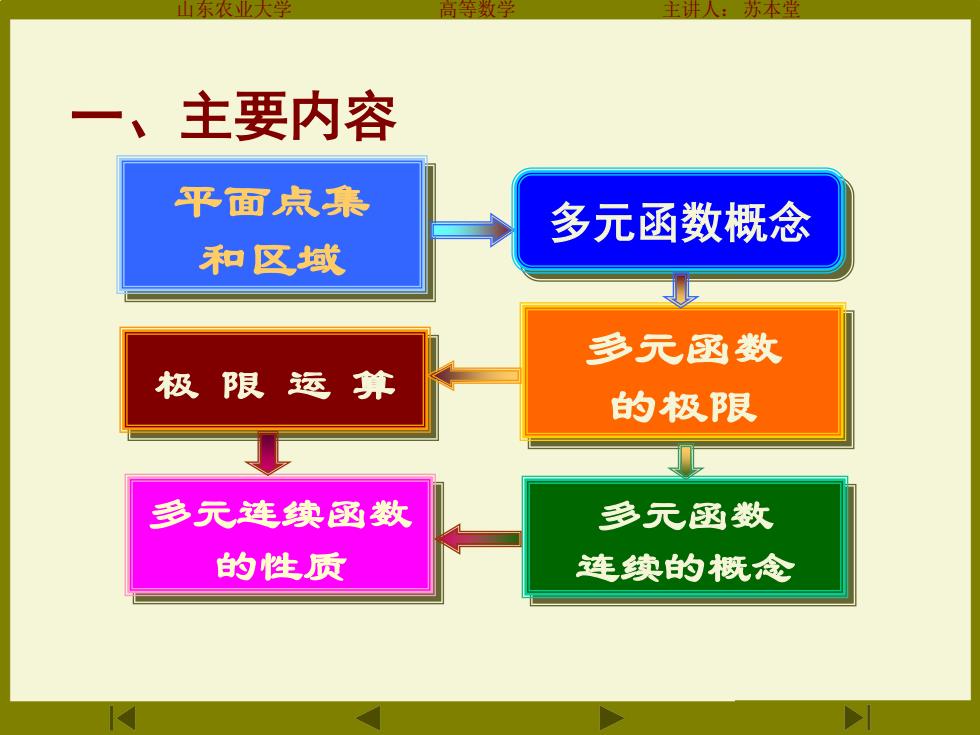
一、主要内容 平面点集 多元函数概念 和区域 多元函数 极限运算 的极限 乡元连续数 多元函数 的性质 连续的概念
山东农业大学 高等数学 主讲人:苏本堂 平面点集 和区域 多元函数 的极限 多元函数 连续的概念 极 限 运 算 多元连续函数 的性质 多元函数概念 一、主要内容

主讲 苏本堂 全微分 方向导数 全微分 的应用 概念 复合函数 高阶偏导数 求导法则 偏导数 全微分形式 概念 隐函数 的不变性 求导法则 微分法在 多元趣数的极值 几何上的应用
山东农业大学 高等数学 主讲人:苏本堂 全微分 的应用 高阶偏导数 隐函数 求导法则 复合函数 求导法则 全微分形式 的不变性 微分法在 几何上的应用 方向导数 多元函数的极值 全微分 概念 偏导数 概念
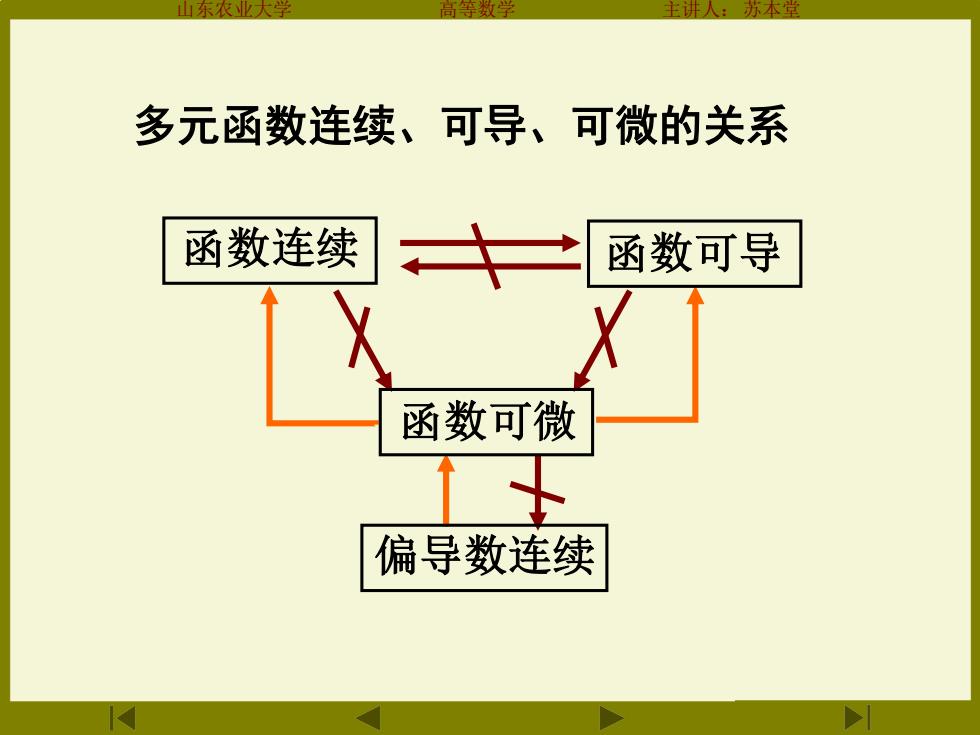
多元函数连续、可导、可微的关系 函数连续 函数可导 函数可微 偏导数连续
山东农业大学 高等数学 主讲人:苏本堂 多元函数连续、可导、可微的关系 函数可微 函数连续 偏导数连续 函数可导

等数学 内容小结 1.区域 ·邻域:U(Po,δ),U(P,δ) ·区域 连通的开集 。R”空间 2.多元函数概念 n元函数u=f(P)=f(x1,x2,.,xn) P∈DcRm 二元函数(图形一般为空间曲面) 常用 三元函数
山东农业大学 高等数学 主讲人:苏本堂 内容小结 1. 区域 • 邻域 : ( ,δ ), U P0 ( ,δ ) U P0 • 区域 连通的开集 • R n空间 2. 多元函数概念 n 元函数 ( , , , ) 1 2 n = f x x x 常用 二元函数 (图形一般为空间曲面) 三元函数 PD u = f (P) n R