
第六节多元函数微分学的几何应用 一、空间曲线的切线与法平面 二、曲面的切平面和法线
山东农业大学 高等数学 主讲人:苏本堂 一、空间曲线的切线与法平面 二、曲面的切平面和法线 第六节 多元函数微分学的几何应用
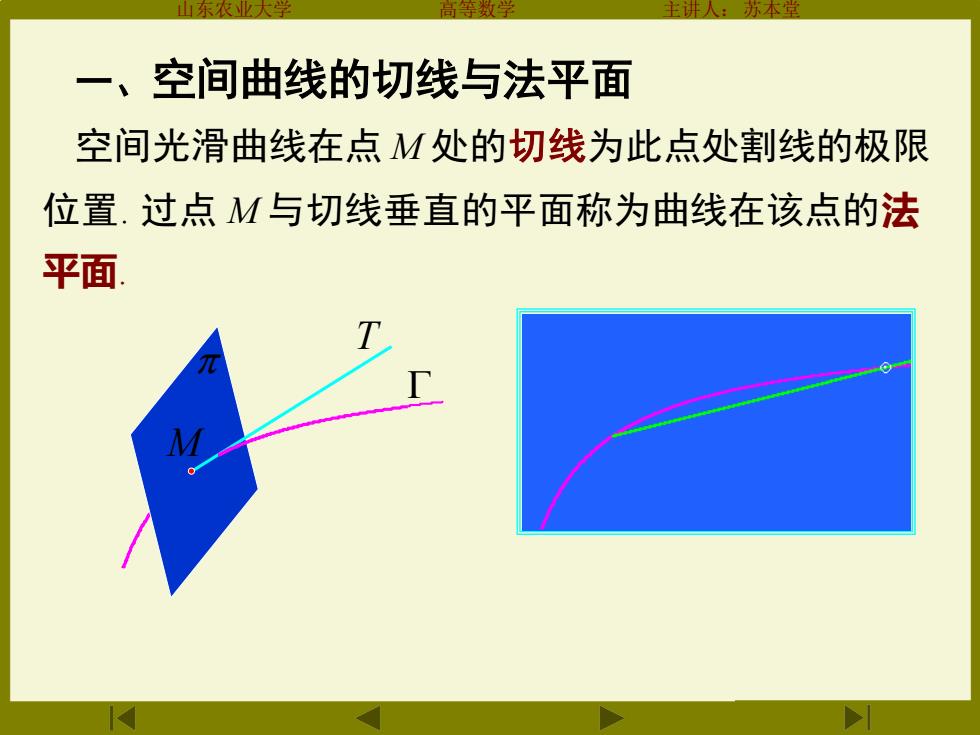
方本 一、空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限 位置.过点M与切线垂直的平面称为曲线在该点的法 平面
山东农业大学 高等数学 主讲人:苏本堂 一、空间曲线的切线与法平面 位置. 过点 M 与切线垂直的平面称为曲线在该点的法 T M 空间光滑曲线在点 M 处的切线为此点处割线的极限 平面
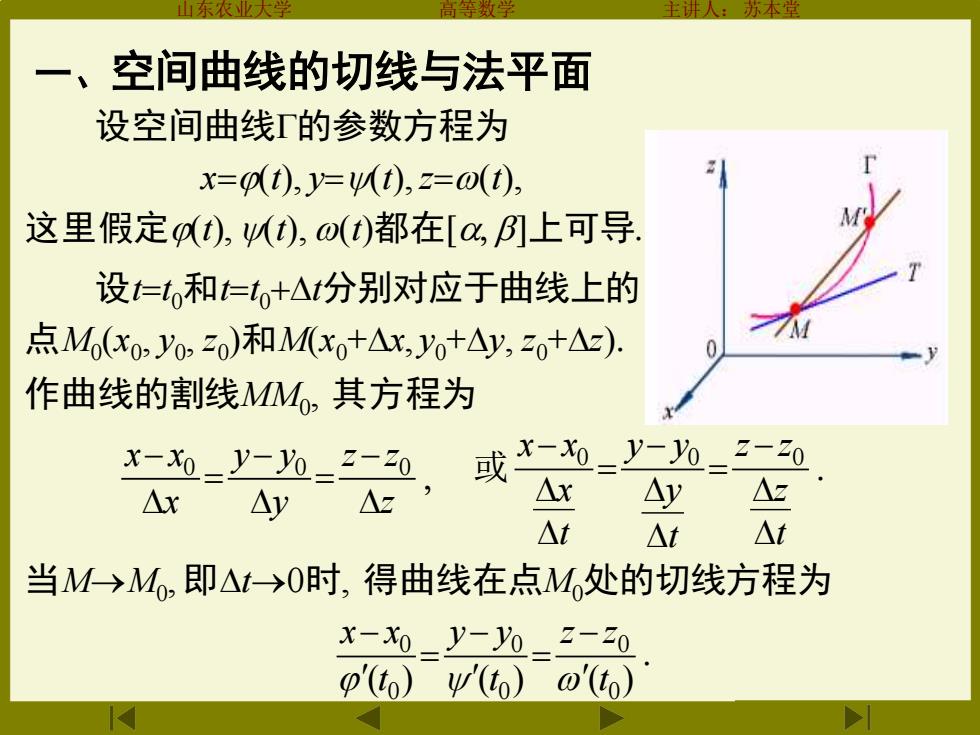
一、 空间曲线的切线与法平面 设空间曲线「的参数方程为 x=0(),y=t),z=0(t0), 这里假定(),(t),o(t)都在[,例上可导 设仁,和仁t+△分别对应于曲线上的 点M(xo,yo2o)和Mx0+△x,y+△y,2o+△): 作曲线的割线MM,其方程为 X-=y-h=-0,或0=y6=-0 △x △y △z △x △y △t △t △t 当M→M,即△t→0时,得曲线在点M处的切线方程为 X-X0_y-y0_2-20 P(to) w() @
山东农业大学 高等数学 主讲人:苏本堂 设空间曲线的参数方程为 x=(t), y=(t),z=(t), 这里假定(t),(t), (t)都在[ ]上可导 设t=t 0和t=t 0+t分别对应于曲线上的 点M0 (x0 , y0 , z0 )和M(x0+x, y0+y, z0+z) 当M→M0 , 即t→0时, ( ) ( ) ( ) 0 0 0 0 0 0 t z z t y y t x x − = − = − z z z y y y x x x − = − = − 0 0 0 或 t z z z t y y y t x x x − = − = − 0 0 0 作曲线的割线MM0 , 其方程为 得曲线在点M0处的切线方程为 z z z y y y x x x − = − = − 0 0 0 或 t z z z t y y y t x x x − = − = − 0 0 0 一、空间曲线的切线与法平面

主讲》 方本堂 一、空间曲线的切线与法平面 设空间曲线「的参数方程为 x=0(t),J=(t),2=0(t), 这里假定0t),(t),o(t)都在[a,]上可导 过曲线厂上=t所对应的点M,切线方 T Mo 程为 X-0-y-y0_2-20 p'(4o)W(o)o'(o) 向量T=(0(to),W(to),o'(to)称为曲线T在点M的切向量 通过点M而与切线垂直的平面称为曲线Γ在点M,处的法 平面,其法平面方程为 0'(to)x-xo)+W(to)0y-yo)+0'(t)(z-20)=0
山东农业大学 高等数学 主讲人:苏本堂 设空间曲线的参数方程为 x=(t) y=(t)z=(t) 这里假定(t),(t), (t)都在[ ]上可导 ( ) ( ) ( ) 0 0 0 0 0 0 t z z t y y t x x − = − = − 过曲线上t=t 0所对应的点M0切线方 程为 向量T=((t 0 ) (t 0 ) (t 0 ))称为曲线在点M0的切向量. 通过点M0而与切线垂直的平面称为曲线在点M0处的法 平面, 其法平面方程为 (t 0 )(x−x0 )+(t 0 )(y−y0 )+(t 0 )(z−z0 )=0 一、空间曲线的切线与法平面

例1.求圆柱螺旋线x=Rcosp,y=Rsinp,z=kp在 P=?对应点处的切线方程和法平面方程, 解:由于x'=-Rsinp,y'=Rcosp,z'=k,当p=号时, 对应的切向量为T=(-R,0,k),故 切线方程 x=y-R_z-3k Mo(0,R,k) -R 0 k 即 kx+Rz-3Rk=0 y-R=0 法平面方程-Rx+k(z-牙k)=0 即 Rx-k=+k2=0
山东农业大学 高等数学 主讲人:苏本堂 z x y o 例1. 求圆柱螺旋线 对应点处的切线方程和法平面方程. 切线方程 = − R x 法平面方程 − R x 0 2 2 R x − k z + k = 即 − = + − = 0 0 2 y R k x Rz Rk 即 解: 由于 0 y − R k z k 2 − = (0, , ) 0 2 M R k 对应的切向量为 ( ) 0 2 + k z − k = 在 T = (−R, 0, k) , 故