
高率 第三节三重积分 一、三重积分的概念 二、三重积分的计算
山东农业大学 高等数学 主讲人:苏本堂 第三节 三重积分 一、三重积分的概念 二、三重积分的计算

一、三重积分的概念 引例:设在空间有限闭区域2内分布着某种不均匀的 物质,密度函数为(x,y,z)∈C,求分布在2内的物质的 质量M. 解决方法:类似二重积分解决问题的思想,采用 “大化小,常代变,近似和,求极限” 可得 M=lim∑4(5,7,5A)△vg △Vk λ→0 k=1 (5k,7k,5k)
山东农业大学 高等数学 主讲人:苏本堂 一、三重积分的概念 类似二重积分解决问题的思想, 采用 k k k k ( , , )v ( , , ) k k k k v 引例: 设在空间有限闭区域 内分布着某种不均匀的 物质, (x, y,z)C, 求分布在 内的物质的 可得 = n k 1 0 lim → M = “大化小, 常代变, 近似和, 求极限” 解决方法: 质量 M . 密度函数为

三重积分的定义 设x,y,)是空间有界闭区域2上的有界函数: 将2任意分成n个小闭区域 △y1,△y2,··,△Vn 其中△y,表示第个小闭区域,也表示它的体积 在每个小闭区域△y,上任取一点(5,S),作和 ∑f(5,1,5)△y· 1 如果当各小闭区域的直径中的最大值趋于零时,这 和的极限总存在,则称此极限为函数孔x,y,z)在闭区域2 上的三重积分,记作川fx,y,2w. dv称为体积元素,在直角坐标系下常写作dxdydz:
山东农业大学 高等数学 主讲人:苏本堂 设f(x y z)是空间有界闭区域上的有界函数 将任意分成n个小闭区域 v1 v2 vn 其中vi表示第i个小闭区域也表示它的体积 在每个小闭区域vi上任取一点(i i i ) 作和 三重积分的定义 i i i i n i f v = ( , , ) 1 如果当各小闭区域的直径中的最大值趋于零时这 和的极限总存在 则称此极限为函数f(x y z)在闭区域 上的三重 积分 记作 f x y z dv ( , , ) dv称为体积元素, 在直角坐标系下常写作 dxdydz

1东农大 主讲人:苏本堂 二、三重积分的计算 1.利用直角坐标计算三重积分 方法1.投影法(先一后二”) 方法2.截面法(先二后一”) 方法3.三次积分法
山东农业大学 高等数学 主讲人:苏本堂 二、三重积分的计算 1. 利用直角坐标计算三重积分 方法1 . 投影法 (“先一后二”) 方法2 . 截面法 (“先二后一”) 方法3 . 三次积分法
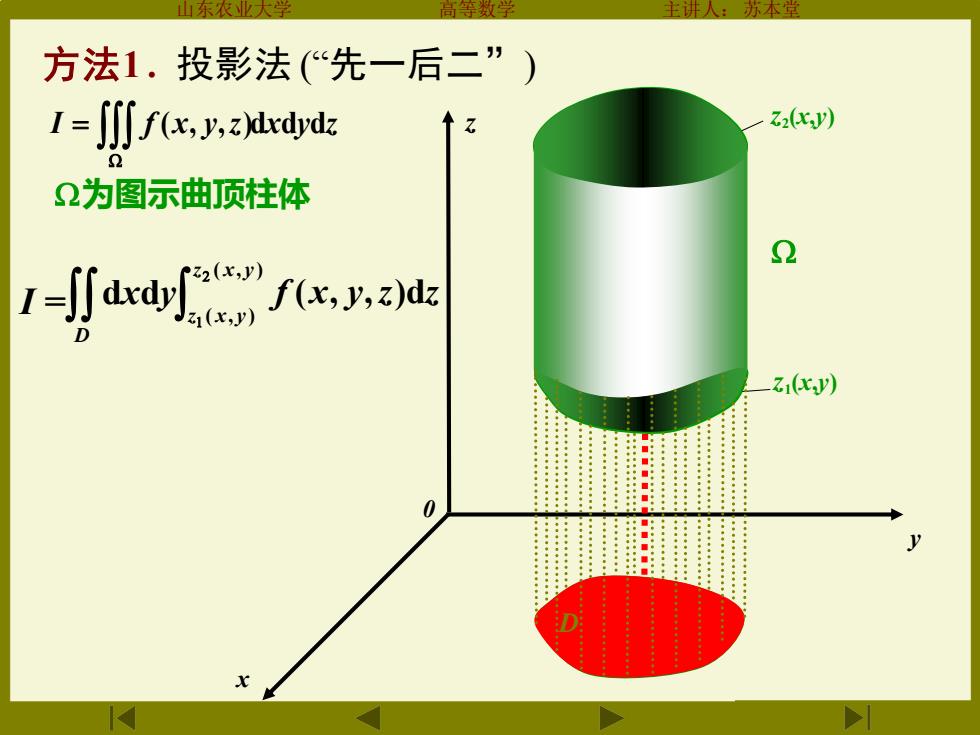
方法1.投影法(先一后二”) I=j∬fx,y.zXlxdydz Z2(xy) Ω为图示曲顶柱体 2 I=∬d时fx,3地 z(xv)
山东农业大学 高等数学 主讲人:苏本堂 x 0 z y z2(x,y) 为图示曲顶柱体 I = ( , ) ( , ) ( , , )d z x y z x y f x y z z D dxdy P N M . . D z1(x,y) I f (x, y,z)dxdydz = 方法1 . 投影法 (“先一后二”)